Lecture 27. Scheme

课程开始新单元：学习编程语言 Scheme

今天的课程将开启新的单元，介绍一门新的编程语言——Scheme。虽然我们已经掌握了 Python 的基础知识，包括函数、数据、对象系统，甚至迭代器和生成器等高级话题，但通过学习 Scheme，可以更深入地理解编程语言的本质，并且看到不同语言之间的相似性。

为什么学习新的编程语言？

• 学习新的编程语言并不仅仅是为了增加工具库，而是为了展示对编程语言如何运作的深刻理解。
• Python 已经提供了丰富的编程功能，学完它后，你已经能够构建各种程序。今天的重点是通过学习 Scheme，展示编程语言背后的一些共同概念。

Scheme 简介

• Scheme 是一门非常简洁的编程语言，属于 Lisp 方言。Lisp 是两大仍然广泛使用的最古老编程语言之一，对 Python 的发展有着深远的影响。
• Lisp 因其历史、简洁性及强大的表达能力广受推崇。例如，面向对象编程的发明者 Alan Kay 称其为 “有史以来设计最好的编程语言”，而许多程序员也赞美其优雅的语法。

Scheme 的基本概念

Scheme 程序由表达式构成，表达式分为以下两类：

• 原始表达式：直接表示数值、运算符等基本单位。例如：2、3.3、+、quotient（表示除法操作）等。
• 组合表达式：由括号包裹的多个表达式组成，形式如 (操作符 操作数1 操作数2 ...)。例如：(quotient 10 2) 计算 10/2，结果为 5。

原始表达式和组合表达式

• 数字是自求值的（即自身就是值），符号则需要绑定到某个值上。
• 调用表达式形如 (操作符 操作数1 操作数2 ...)，这与 Python 不同。在 Python 中，操作符放在函数外部，而在 Scheme 中，操作符位于括号内。

Scheme 中的调用表达式示例

1. 简单的除法操作：在 Scheme 提示符下输入 (quotient 10 2)，结果是 5。quotient 是内建的整数除法过程。
   • 在 Python 中，我们称这些为“函数”，而在 Scheme 中，它们被称为“过程”（procedure），但两者本质相同。
2. 嵌套的调用表达式：我们可以嵌套调用表达式。例如，计算 (quotient (+ 8 7) 5)，结果是 3，因为 (+ 8 7) 结果为 15，再除以 5 得到 3。
   • Scheme 的表达式可以跨多行书写，通过适当的缩进提高可读性，但解释器对换行和空格并不敏感。

课程安排调整

• 实验与作业：实验将延迟到周三提交（通常是周二），因为美国本周有选举活动，作业也相应简化。
• 期中考试二的重评分：如果有需要，请在周一之前提交重评分请求。
• Scheme 环境设置：推荐使用 code.cs61a.org，在线加载 Scheme 解释器，快速体验 Scheme 代码执行。

学习 Scheme

Scheme 语言的优雅性在于其极简的设计——一天之内即可掌握全部语言特性，但可以用它构建复杂的程序。从 Python 迁移到 Scheme 的过程也能帮助我们理解编程语言中的共性概念，并培养更强的抽象能力。

在 Scheme 中，程序通过组合表达式构造，其中表达式可以跨越多行，并通过适当的缩进提高可读性。尽管缩进和空格对于人类阅读很重要，但对解释器并不重要。唯一需要注意的是，每个打开的括号必须有相应的关闭括号。

我们可以通过一个例子来理解组合表达式的工作方式。假设有一个表达式：
(+ (* 3 (+ (* 2 4) (+ 3 5))))
这个表达式的含义是：

1. 内层表达式先计算乘法：(* 2 4)，结果是 8；
2. 然后将 3 和 5 相加，得到 8；
3. 将两个 8 相加，得到 16；
4. 最后，16 乘以 3，结果是 48。

再举一个例子：
(+ (- 10 7) 6)
这里，(- 10 7) 先计算，结果是 3，再加上 6，结果是 9。

Scheme 交互式解释器示例

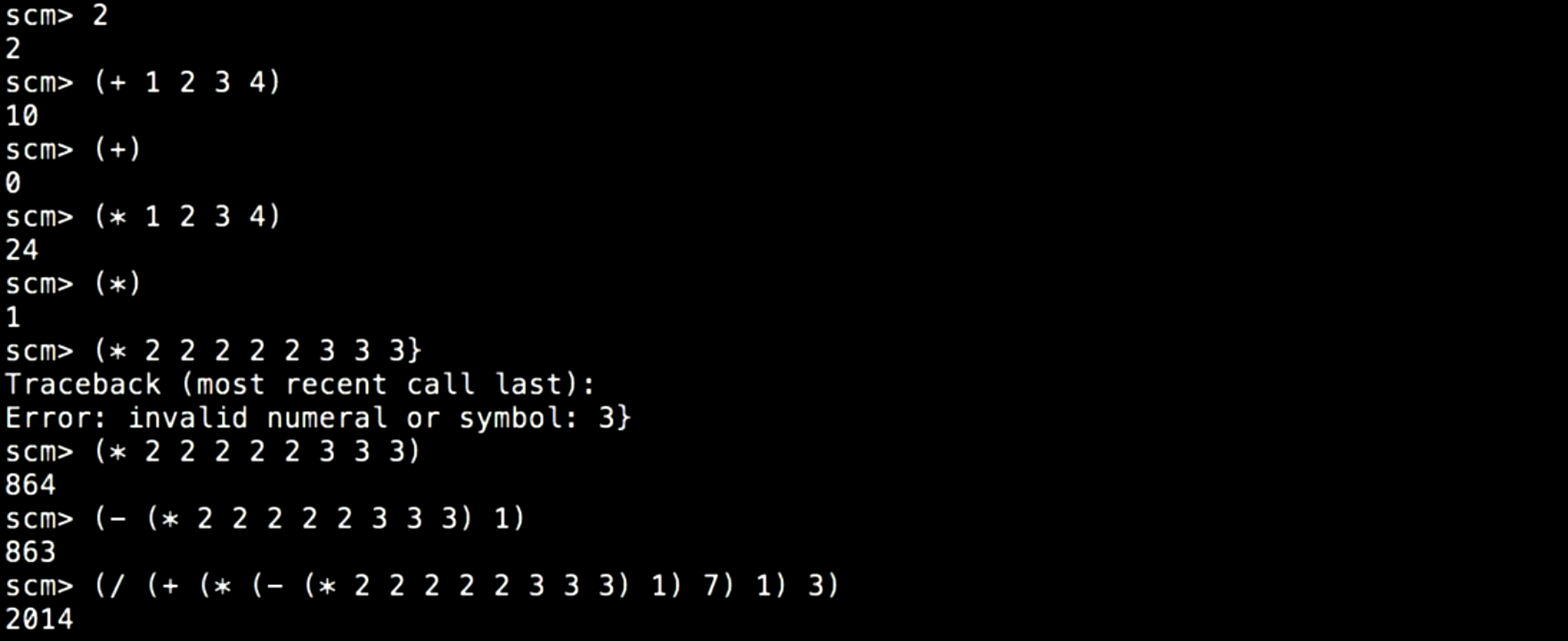
• 我们可以在 Scheme 提示符下直接输入数字或表达式进行计算。例如，输入 2 将返回 2。
• 输入 (+)，即不传递任何参数给加法操作，结果是 0，因为空加法返回零。同样，空乘法返回 1。

其他示例包括：

• (* 1 2 3 4) 计算结果是 24。
• 嵌套表达式 (- (* 2 2 2 2 3 3 3) 1) 计算结果是 864 - 1 = 863。

在 Scheme 中，组合表达式的评估过程与 Python 基本相同，只是括号的使用方式有所不同。

Scheme 内置过程

Scheme 还提供了一些内置过程，除了数学运算之外，还有其他类型的检查。例如：

• (number? 3) 返回 #t，表示 3 是一个数字。
• (number? +) 返回 #f，表示 + 不是数字。
• (zero? 2) 返回 #f，表示 2 不是零。
• (zero? 0) 返回 #t，表示 0 是零。
• (integer? 2.2) 返回 #f，因为 2.2 不是整数。
• (integer? 2) 返回 #t，表示 2 是整数。

其中带有问号的名称表示这些过程返回布尔值（#t 或 #f），例如 integer? 就是一个判断是否为整数的过程。

特殊形式（Special Forms）

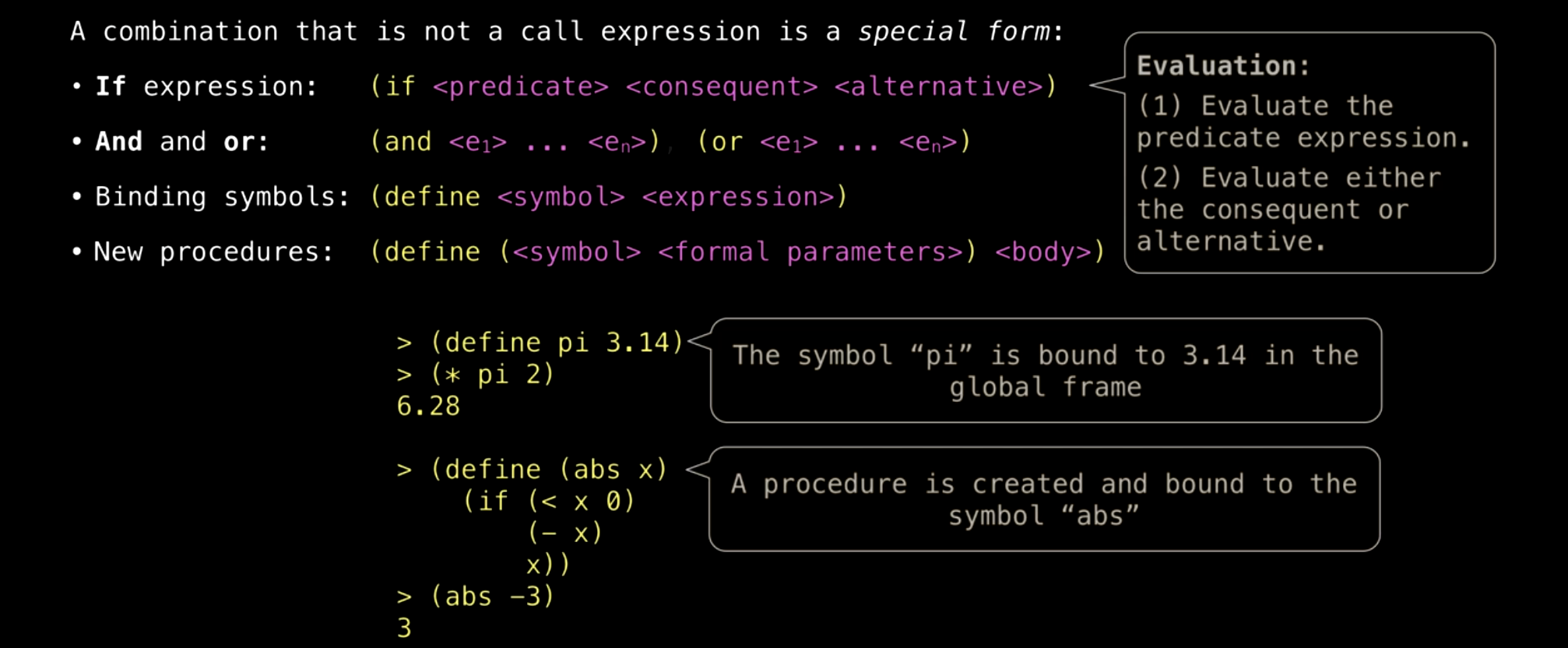
除了调用表达式，Scheme 中还有一些特殊形式，它们的表现方式不同于一般的调用表达式：

• if 表达式：
  语法类似于组合表达式，但首个子表达式是 if 关键字，接着是谓词、后继和替代表达式。根据谓词的真假，决定评估后继或替代表达式。
  例子：(if (< x 0) (- x) x) 表示如果 x 小于 0，返回 -x，否则返回 x。

• 逻辑运算符 and 和 or：
  它们也属于特殊形式，可以短路评估，意味着有时不需要评估所有子表达式即可确定结果。

• define 表达式：
  用于将某个值绑定到符号。例如：
  (define pi 3.14) 将符号 pi 绑定到值 3.14，之后可以在其他表达式中使用 pi。

定义过程

在 Scheme 中，还可以定义过程（类似 Python 中的函数）。定义过程时，使用 define 关键字，但其语法与绑定值有所不同：

• 例如，定义绝对值函数：

  (define (abs x)
    (if (< x 0)
        (- x)
        x))
  

  这里，abs 是过程的名称，x 是形式参数。每次调用 abs 时，Scheme 会检查 x 是否小于 0，如果是，则返回 -x，否则返回 x。

通过学习 Scheme 的这些基础概念，我们可以看到与 Python 类似的调用过程和符号绑定模型。

在 Scheme 中，每次调用 abs 函数时，它会评估主体表达式：如果传入的参数 x 小于零，则返回 -x，否则返回 x。这是典型的 if 表达式，它由谓词、后继和替代表达式组成。如果我们计算 abs 3，结果是 3。这个 define 表达式创建了一个新的过程，并将符号 abs 绑定到当前环境的第一个帧（在全局环境中）。

接下来，我们可以自己定义一些过程。例如，定义一个平方函数：

(define (square x)
  (* x x))

调用 (square 16) 将得到 256。再定义一个计算平均值的函数：

(define (average x y)
  (/ (+ x y) 2))

调用 (average 3 7) 将返回 5。在 Scheme 中，我们已经知道如何评估调用表达式，而且这些表达式可以嵌套，递归函数也非常常见。

递归定义示例：平方根计算

让我们定义一个递归函数来计算平方根。我们首先需要定义一个更新函数来改进猜测值：

(define (update guess x)
  (if (= (* guess guess) x)
      guess
      (average guess (/ x guess))))

这个函数会检查猜测的平方是否等于我们要求的数 x，如果是，则返回当前猜测值，否则更新猜测值。更新过程通过巴比伦方法（Babylonian method），即计算当前猜测和 x 除以当前猜测的平均值。

然后定义一个函数来不断更新猜测，直到找到平方根：

(define (sqrt x)
  (define (update guess)
    (if (= (* guess guess) x)
        guess
        (update (average guess (/ x guess)))))
  (update 1))  ; 从猜测值1开始

调用 (sqrt 256) 将返回 16。在这个例子中，我们利用了许多 Scheme 的特性，包括嵌套的过程定义。在 Scheme 中，和 Python 一样，使用的是词法作用域（lexical scoping），因此在内部函数体中可以引用外部函数的参数 x。

如何执行 Scheme 代码？

虽然可以下载 Scheme 解释器或在线使用嵌入网页的解释器，但在本课程的项目中，我们将实现自己的 Scheme 解释器。通过构建一个 Python 程序来实现 Scheme 解释器，你可以执行 Scheme 代码。这个项目的目的是帮助我们更深入地理解编程语言的构建方式。

Lambda 表达式

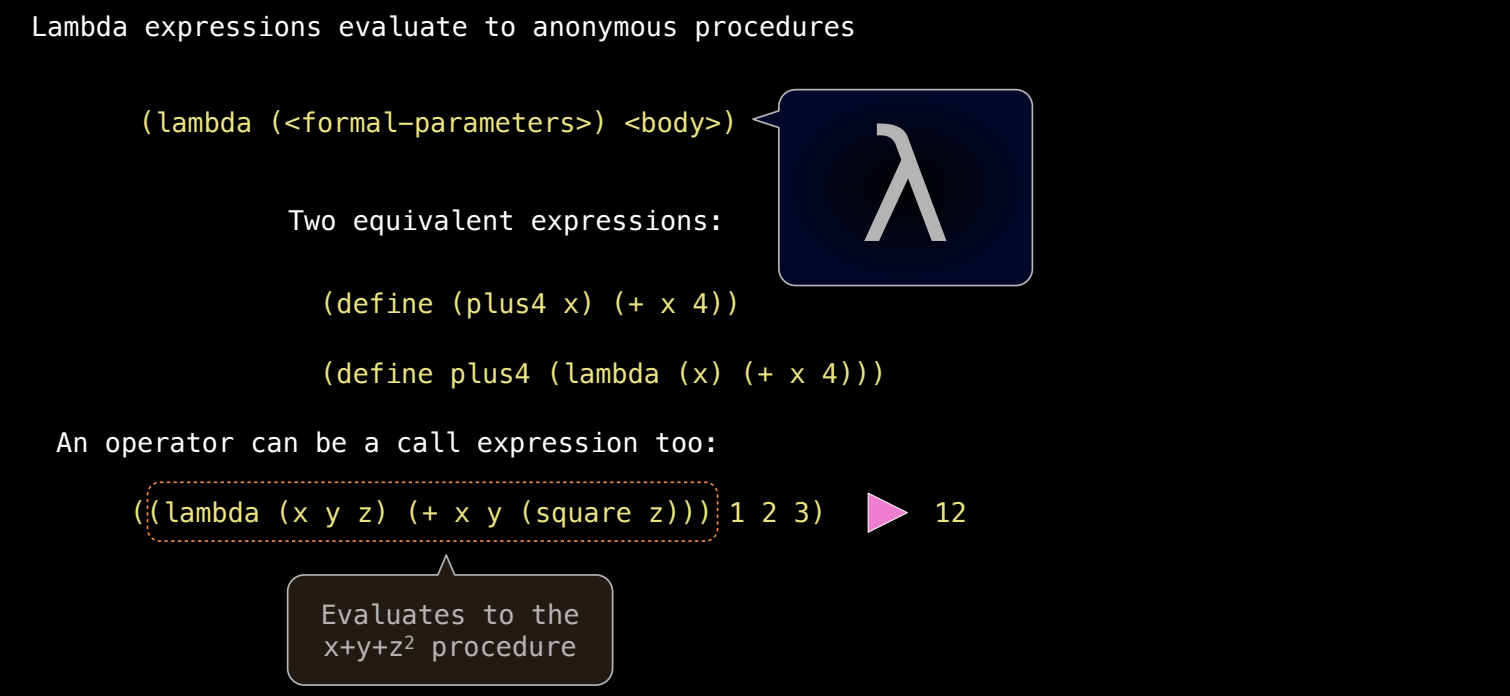
在 Scheme 中，lambda 表达式用于创建匿名过程。语法为：

(lambda (参数列表) 过程主体)

例如，定义一个加 4 的过程：

(define plus-four (lambda (x) (+ x 4)))

这等价于：

(define (plus-four x)
  (+ x 4))

这两种方式是等效的，Scheme 允许你以灵活的方式定义过程。你可以在调用表达式中使用组合的操作符，例如，计算 1 + 2 + 3^2：

((lambda (x y z) (+ x y (* z z))) 1 2 3)  ; 返回 12

使用 Scheme 画图：Sierpinski 三角形

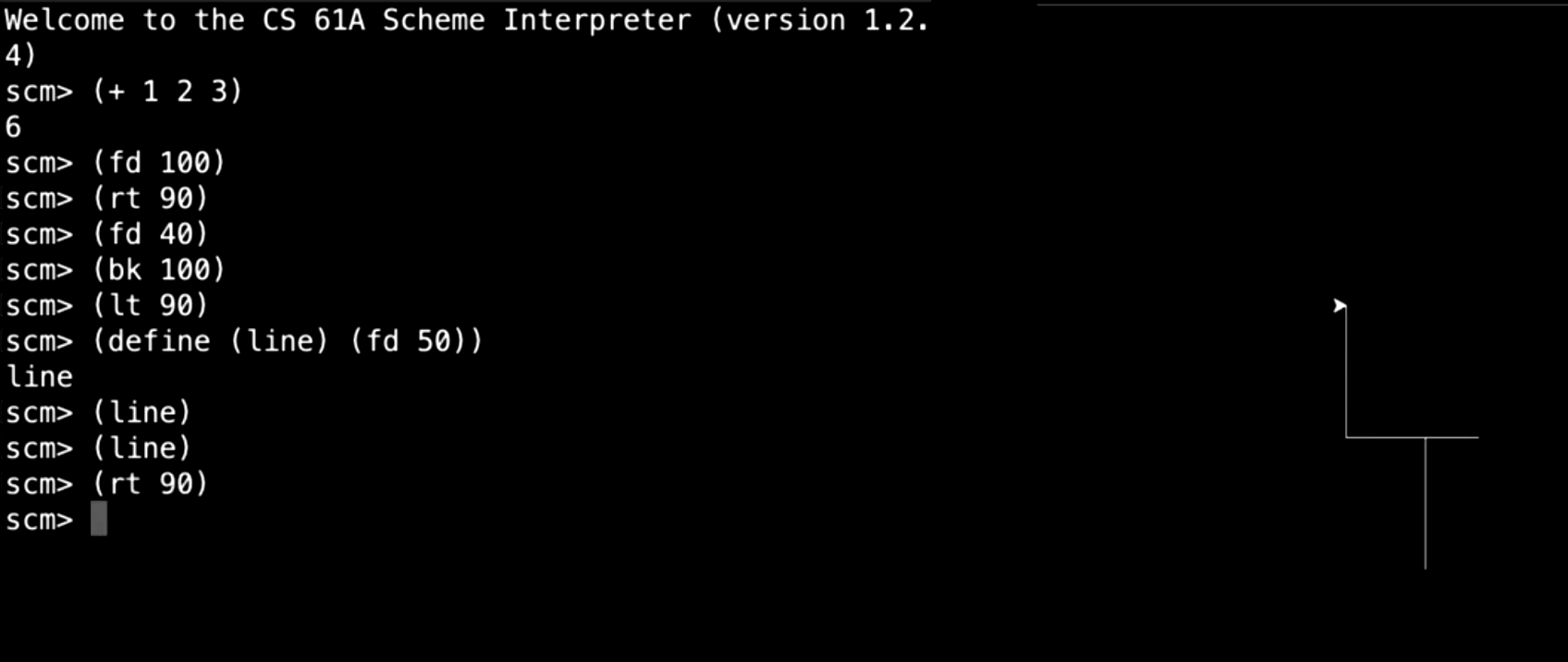
CS 61A Scheme Interpreter 中内置了一些绘图功能。可以通过 forward 命令让小海龟前进一定的距离：

(forward 100)

然后可以让海龟右转 90 度，再次前进，或者通过 backward 命令后退。定义一个简单的画线过程：

(define (draw-line)
  (forward 50))

也可以定义一个过程执行某个动作两次：

(define (do-twice action)
  (action)
  (action))

调用 (do-twice draw-line) 会画两条线。

我们可以使用递归或重复的方式来绘制更复杂的图形。

一个例子是创建一个重复执行某个操作的过程，例如 repeat，它允许我们重复某个过程若干次。假设我们想重复执行绘制线段和右转的操作，可以通过以下方式定义：

(define (repeat k fn)
  (fn)
  (if (> k 1)
      (repeat (- k 1) fn)))

这个 repeat 过程将调用某个过程 k 次，并且每次递归地减少计数 k。

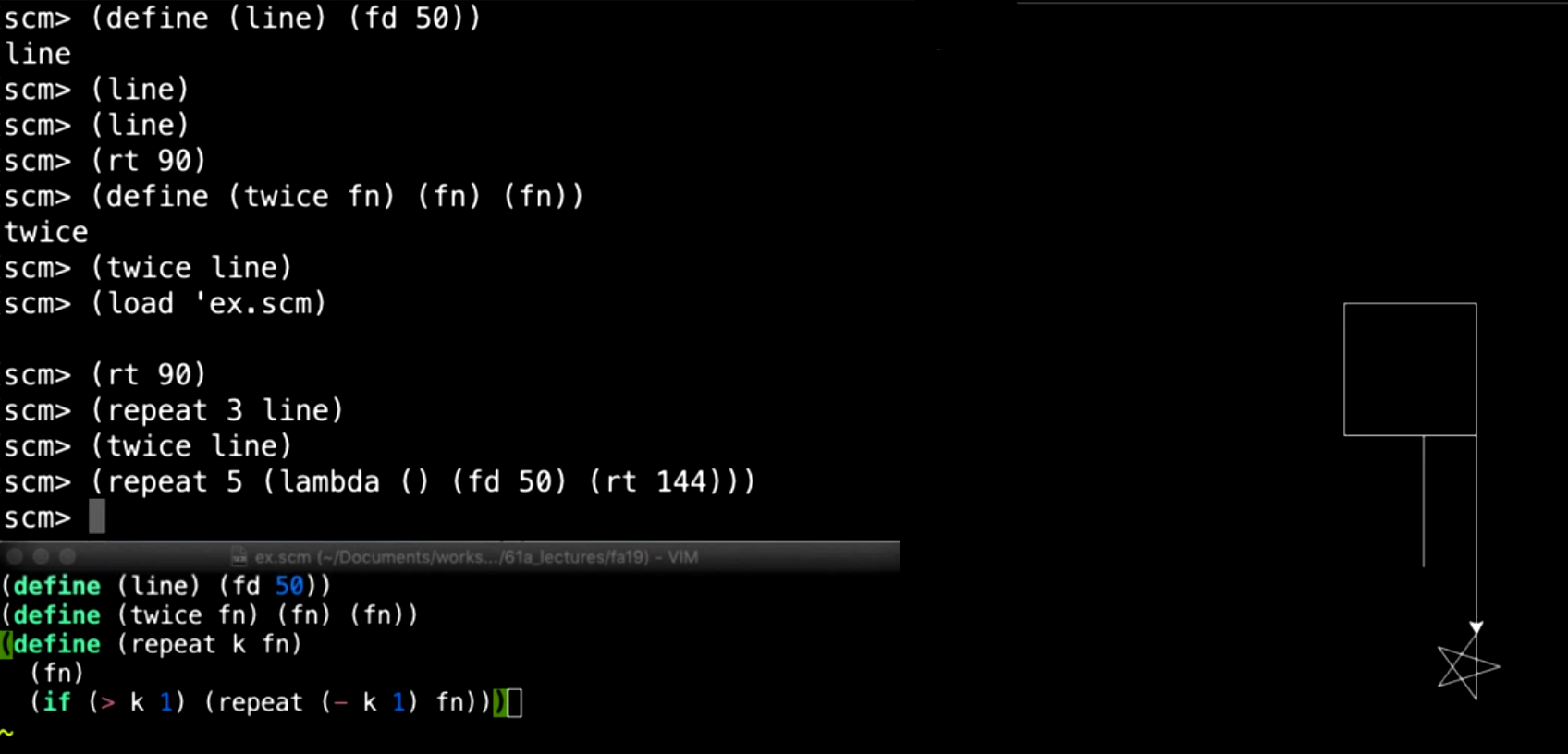
函数的递归条件是，当 k > 1 时，继续递归调用 repeat，每次 k 减少 1，直到 k 等于 1。例如，(repeat 5 line) 会调用 line 函数 5 次。

如果我们希望画一个多边形，例如五边形，可以通过以下方式实现：

(repeat 5
        (lambda ()
          (forward 50)
          (turn-right 144)))

这个例子中，lambda 定义了一个没有参数的匿名过程，每次执行时海龟向前移动 50 单位并右转 144 度，重复 5 次则会形成一个五边形。

Sierpinski Triangle 绘制过程讲解

现在我们已经知道如何使用递归绘制图形了，所以我们可以先从简单的例子开始，例如画一个三角形。这个三角形很简单，只需要重复三次画边的操作，再加上每次向左转 120 度，这样就可以完成一个等边三角形的绘制。然而，这样的三角形显得非常普通，仅仅是一个用直线作为边的三角形。

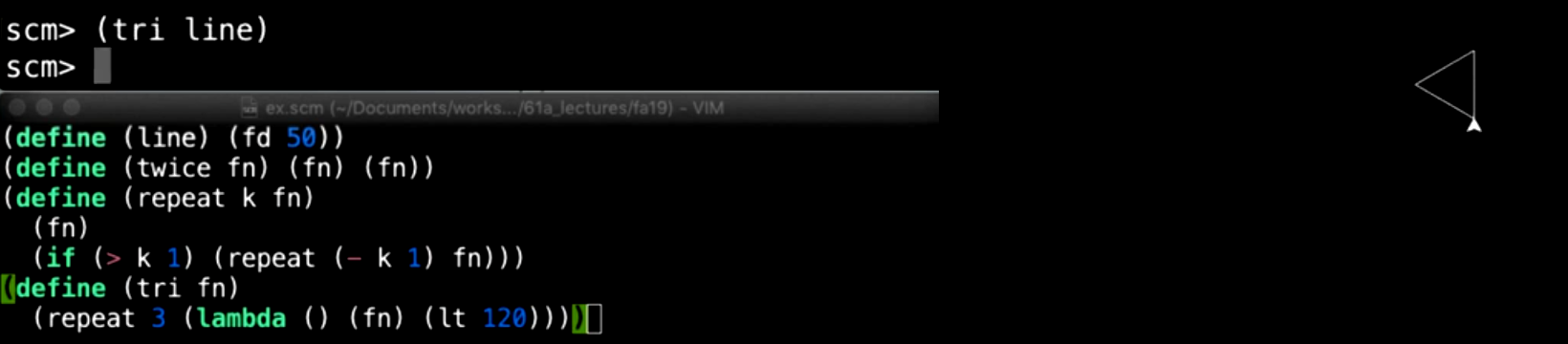
但是，我们不想画这样一个简单的三角形。为了增加复杂度和趣味性，我们希望定义一个可以有任意边形样式的三角形。为了实现这一点，我们可以使用函数来定义什么叫做绘制三角形的边。虽然三角形的基本绘制仍然是重复三次，但是边的具体绘制方法则由函数来控制，而每次边的绘制之后再向左转 120 度。

(define (tri fn)
  (repeat 3 (lambda () (fn) (lt 120))))

接下来，我们引入了一个更复杂的三角形，即谢尔宾斯基三角形（Sierpinski Triangle）。它是一个递归的分形结构，具有一些复杂的递归深度 d 和边长 k。

谢尔宾斯基三角形定义

谢尔宾斯基三角形仍然是三角形，但它的边的绘制方式不再是简单的直线。绘制这个三角形的边涉及一个决策过程：

• 如果 d 等于 1，那么我们只是画一条长度为 k 的线，这就是最简单的情况（递归的基线条件）。
• 如果 d 大于 1，我们就需要递归地绘制谢尔宾斯基三角形的腿（leg），每条边实际上是更小的谢尔宾斯基三角形。这里的递归是相互递归的，sier 调用 leg，而 leg 又调用 sier。

绘制递归过程

当我们开始绘制时，每次递归都会执行以下步骤：

1. 递归调用 sier：当深度 d > 1 时，我们不会简单地画一条直线，而是递归调用 sier 去绘制更小的谢尔宾斯基三角形。
2. 绘制腿（leg）：这个过程要求我们先画出一个深度 d-1 的谢尔宾斯基三角形，边长为 k/2。
3. 移动画笔：在绘制每一条边时，我们需要控制画笔的位置。为了移动到新的位置而不画线，我们会使用提笔（penup），移动画笔到正确的位置，再使用落笔（pendown）继续绘制下一个部分。

代码解析

(define (sier d k)
  (if (= d 1)
      (fd k)  ; 如果深度 d 为 1，直接画长度为 k 的边
      (leg d k)))  ; 否则绘制腿，递归调用 leg

(define (leg d k)
  (sier (- d 1) (/ k 2))  ; 绘制更小的谢尔宾斯基三角形
  (penup)  ; 提笔，移动到下一条边的位置
  (fd k)   ; 向前移动 k
  (pendown))  ; 落笔，准备继续绘制

递归绘制效果

在递归的每一层中，三角形会变得越来越小，边长减半，递归深度减少 1，直到我们到达基线条件，即 d = 1。此时，绘制最小的基本三角形，这就是我们所看到的谢尔宾斯基三角形的最基本结构。

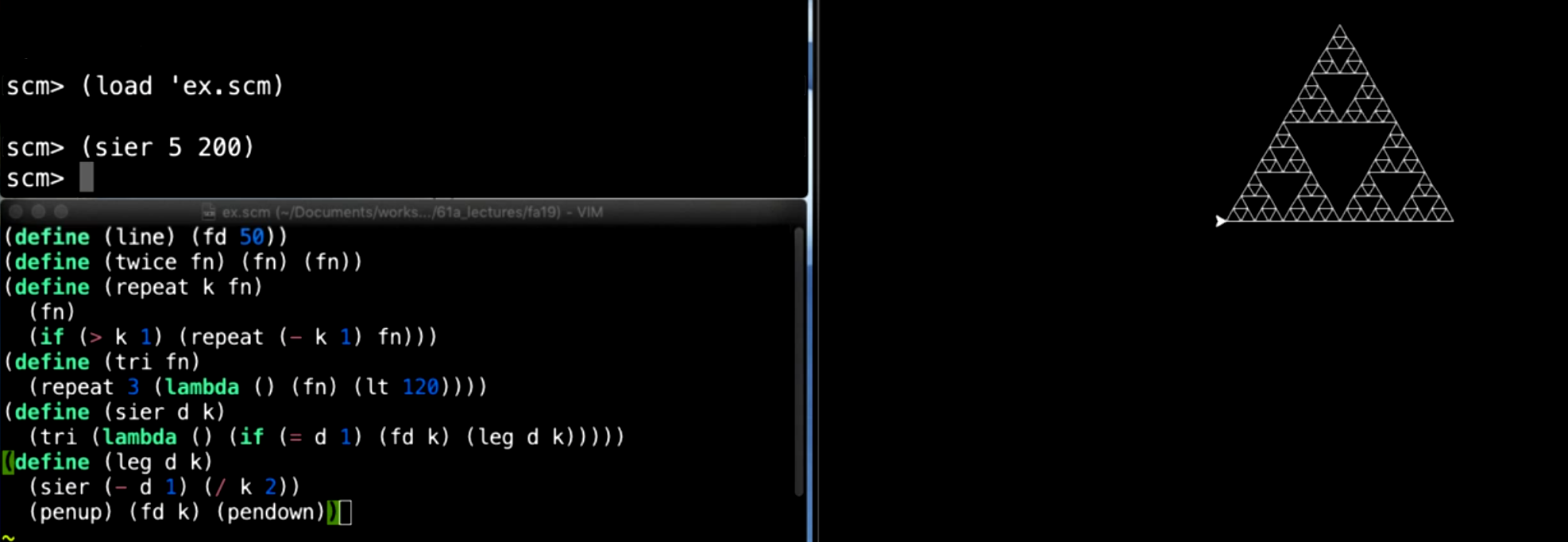
完整绘制流程

1. 开始：我们从一个基本的 90 度右转开始，以设置初始方向。
2. 设置速度：将绘制速度设为 0，表示让图形尽可能快地画出来。
3. 递归绘制：调用 sier 5 200 来绘制递归深度为 5，边长为 200 的谢尔宾斯基三角形。
4. 加载定义文件：在绘制之前，我们需要确保已加载定义谢尔宾斯基三角形的代码文件，以便调用 sier 和 leg 函数。
5. 图形生成：每个小三角形的绘制是递归的基线条件 d = 1，一旦递归结束，我们最终得到整个复杂的分形图案。

递归细节

• 递归的相互调用：sier 函数不仅调用自身，还调用了 leg，而 leg 又调用 sier。这种递归调用模式确保了三角形的边是由更小的谢尔宾斯基三角形构成的。
• 三角形分解：谢尔宾斯基三角形是由三个更小的谢尔宾斯基三角形组成的，而这些小三角形中的每一个又由三个更小的三角形组成，这个过程不断递归，直到到达最小的基本三角形。

最后一步

当所有的递归调用完成后，程序会处理最后的细节：画笔会从绘制的最后一个小三角形逐步回到起点。在返回的过程中，程序会执行所有递归过程中提笔和落笔的操作，确保画笔回到最初的位置。

最终，这样的递归生成了一个复杂而美丽的分形结构。

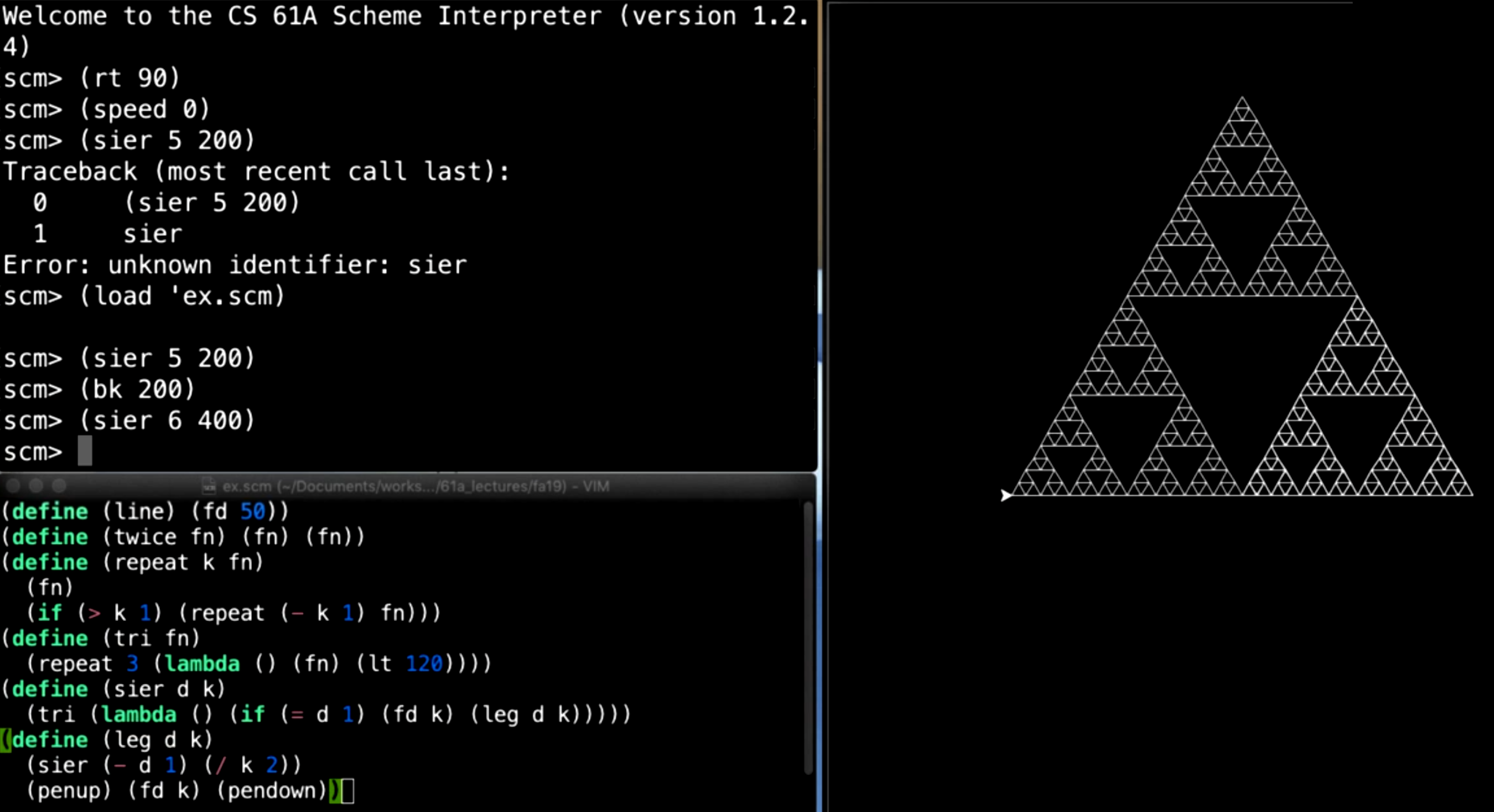
上图展示了一个使用 Scheme 语言编写的递归绘图程序，右侧生成了一个著名的谢尔宾斯基三角形（Sierpinski Triangle）的图形。左侧是代码的定义和交互式执行过程，绘图命令通过递归调用生成了图形。

代码解析

1. (define (repeat k fn) (fn) (if (> k 1) (repeat (- k 1) fn))):
   • 定义了一个递归函数 repeat，用于重复执行 fn 函数 k 次。递归的基线条件是 k > 1，每次递归调用时，k 递减，直到 k 等于 1 为止。

    (define (repeat k fn)
      (fn)
      (if (> k 1)
          (repeat (- k 1) fn)))
   

2. (define (tri fn) (repeat 3 (lambda () (fn) (lt 120)))):
   • 这个函数 tri 用于绘制一个三角形。它使用了 repeat 3 来重复绘制三条边（通过调用 fn，该函数传入的可能是 line），并且在每次画完一条边后，左转 120 度（lt 120），从而形成一个正三角形。

    (define (tri fn)
      (repeat 3 (lambda () (fn) (lt 120))))
   

3. (define (sier d k) (if (= d 1) (fd k) (leg d k))):
   • 这是谢尔宾斯基三角形的递归定义函数。d 表示递归深度，k 表示边的长度。当 d 等于 1 时，直接画一条边（fd k）。
   • 如果 d > 1，则调用 leg 函数，继续递归绘制更小的三角形。

    (define (sier d k)
      (if (= d 1)
          (fd k)
          (leg d k)))
   

4. (define (leg d k) (sier (- d 1) (/ k 2)) (penup) (fd k) (pendown)):
   • leg 函数负责绘制每条递归的“腿”，即在谢尔宾斯基三角形的某个边上再递归绘制一个小三角形。
   • 首先递归调用 sier，并且深度减少 1，长度减半。
   • 然后使用 penup（提笔）和 pendown（落笔）来控制画笔的移动，这样在绘制过程中可以跳过某些位置而不绘制线条。

    (define (leg d k)
      (sier (- d 1) (/ k 2))
      (penup) 
      (fd k)
      (pendown))
   

执行过程

1. 加载文件：代码中执行了 (load 'ex.scm)，表示从文件中加载定义好的 Scheme 函数。

    scm> (load 'ex.scm)
   

2. 绘制谢尔宾斯基三角形：

   • (sier 5 200)：递归深度为 5，边长为 200 的谢尔宾斯基三角形。这在右侧窗口中绘制了一个较大且复杂的谢尔宾斯基三角形。

     scm> (sier 5 200)
     

   • (bk 200)：退回画笔 200 个单位。

     scm> (bk 200)
     

   • (sier 6 400)：递归深度为 6，边长为 400 的谢尔宾斯基三角形。这是一个更大、更复杂的三角形。

     scm> (sier 6 400)
     

图形生成

• 右侧的图形是通过递归调用 sier 函数生成的谢尔宾斯基三角形。该图形由多个较小的等边三角形组成，每个三角形内部又包含更小的三角形，形成了分形结构。

总结

• 递归绘图：谢尔宾斯基三角形的图形结构是一个经典的分形图形，通过递归来实现不断嵌套的等边三角形。
• Scheme 的递归调用：sier 和 leg 函数展示了如何使用递归来绘制复杂的分形结构。通过将边长和递归深度逐步减少，函数递归地构建更小的三角形，直至到达基线条件。
• 画笔控制：使用了 penup 和 pendown 控制画笔的提起和落下，使得程序能够精确控制哪些部分需要绘制，哪些部分需要跳过。

其他特殊形式

cond & begin

除了基本的过程定义和递归之外，Scheme 还有一些特殊形式，如 cond 和 begin。

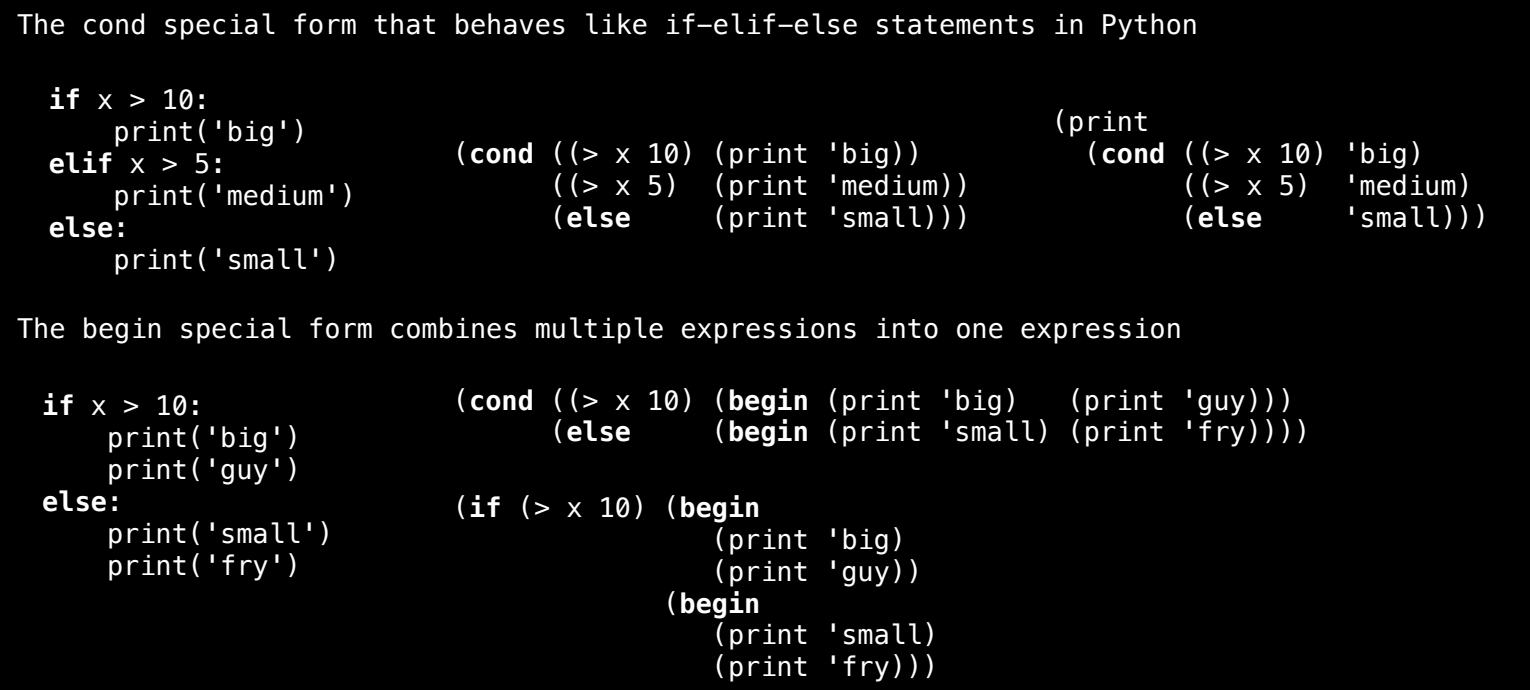
cond 特殊形式类似于 Python 中的 if-elif-else 结构。它允许我们根据多个条件执行不同的操作，而无需嵌套多个 if。其语法为：

(cond
  ((> x 10) (display "big"))
  ((> x 5)  (display "medium"))
  (else     (display "small")))

在这个例子中，cond 检查 x 的值，首先判断是否大于 10，如果是则输出 “big”；否则检查是否大于 5，并输出 “medium”；最后如果都不满足，则输出 “small”。只有一个条件会触发，这与 Python 中的 if-elif-else 行为相同。

begin 特殊形式用于在一个表达式中顺序执行多个操作。例如：

(begin
  (display "Hello, ")
  (display "world!"))

begin 将依次执行其内部的表达式，从而输出 “Hello, world!”。

如果我们需要在 if 的分支中执行多个操作，可以使用 begin：

(if (> x 10)
    (begin
      (display "big")
      (display "guy"))
    (begin
      (display "small")
      (display "fry")))

这里，如果 x 大于 10，则依次执行两个 display，否则执行另一个分支中的两个 display。在Python中如下。

if x > 10:
   print('big')
   print('guy')
else:
   print('small')
   print('fry')

let 特殊形式

let 类似于 define，但它只在某个表达式的范围内临时绑定符号到某个值。绑定结束后，这些符号的值就会消失。相比之下，define 的符号绑定是全局的或持久的。let 常用于临时计算某些值。

例如，我们可以用 let 来计算直角三角形的斜边：

(let ((a 3)
      (b 4))
  (sqrt (+ (* a a) (* b b))))

在这个表达式中，a 被绑定到 3，b 被绑定到 4，计算结果是 5。但是，a 和 b 只在 let 表达式中存在，表达式结束后它们的绑定就会消失。

Scheme 中的列表和 cons

Scheme 中的列表是链表，每个列表由 cons 构造。cons 是一个二元过程，它将两个元素合并为一个链表节点：

(cons 1 '(2 3))  ; 返回 (1 2 3)

car 和 cdr 是两个常用的过程：

• car 返回列表的第一个元素。
• cdr 返回列表的剩余部分。

例如：

(car '(1 2 3))  ; 返回 1
(cdr '(1 2 3))  ; 返回 (2 3)

构建一个包含元素 2 的单元素链表，可以这样写：

(cons 2 nil)  ; 返回 (2)

这个表达式构建了一个包含 2 的单元素链表，其中 nil 表示链表的末尾，是空列表的表示形式，相当于 Python 中的空列表 []。链表的结构通常用这样的方式表示：链表中的第一个元素指向链表的剩余部分，直到 nil 为止。

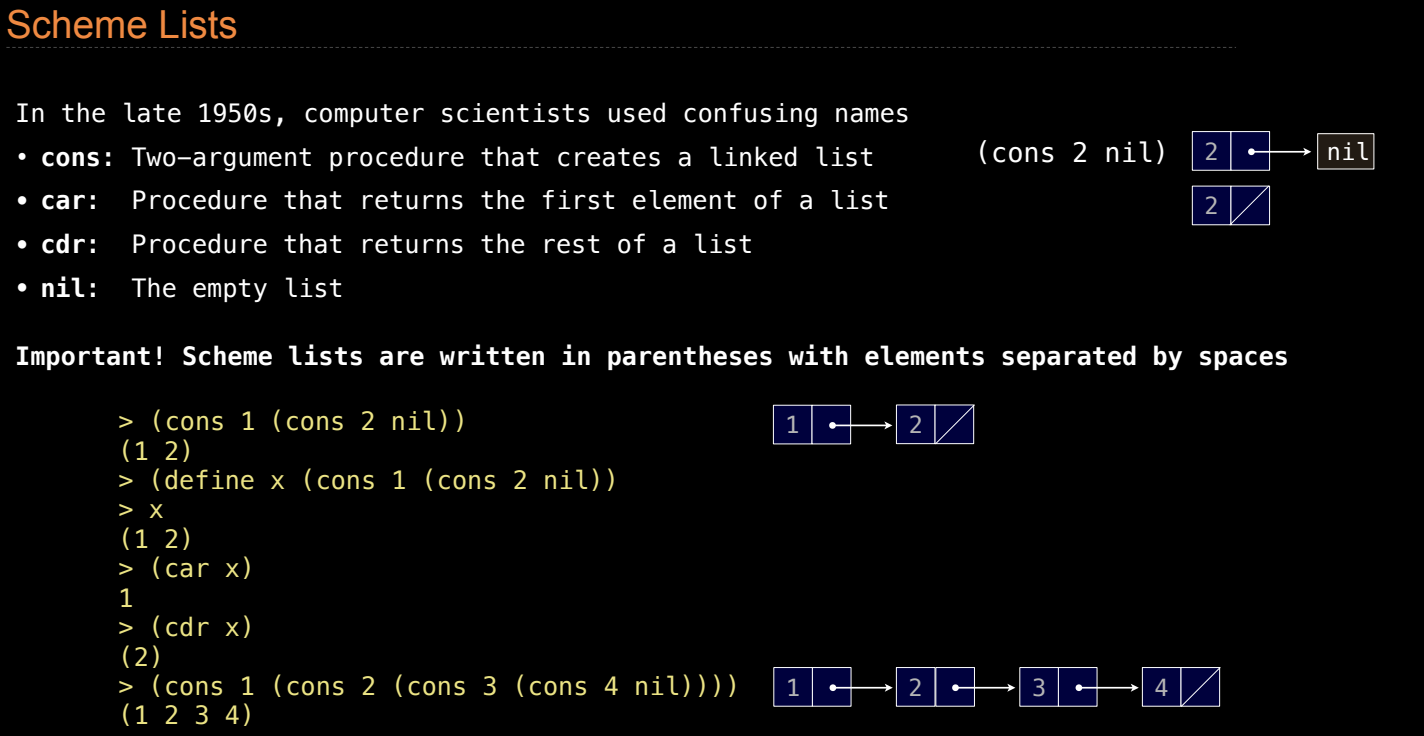
Scheme 中的链表展示方式

虽然链表的底层结构是通过 cons 构建的，但在 Scheme 中链表通常显示为括号内的元素，以空格分隔。例如：

(cons 1 (cons 2 nil))  ; 返回 (1 2)

这表示链表的第一个元素是 1，第二个元素是 2，末尾是 nil。cons 的嵌套结构会被简化为 (1 2) 的列表表示形式。

假设我们定义一个包含 1 和 2 的链表：

(define x (cons 1 (cons 2 nil)))

• (car x) 返回 1，这是链表的第一个元素。
• (cdr x) 返回 (2)，即链表的剩余部分。

进一步构建更长的链表：

(cons 1 (cons 2 (cons 3 (cons 4 nil))))  ; 返回 (1 2 3 4)

在这个链表中，1 是第一个元素，(2 3 4) 是剩余部分。

更复杂的链表结构

我们可以构建嵌套的链表。例如：

(cons (cons 4 (cons 3 nil)) (cons 1 (cons 2 nil)))  ; 返回 ((4 3) 1 2)

在这个例子中，(4 3) 是链表的第一个元素，它本身也是一个链表。显示结果为 ((4 3) 1 2)，而其底层结构则是链表的嵌套结构。

如果我们想查看链表的第一个元素：

(car (cons (cons 4 (cons 3 nil)) (cons 1 (cons 2 nil))))  ; 返回 (4 3)

car 返回的是链表的第一个元素，即嵌套的 (4 3)。

引用相同的列表

我们还可以在同一个链表中引用同一个子列表。例如：

(cons x (cons x nil))  ; 返回 ((1 2) (1 2))

这里，链表的两个元素都是同一个列表 x，即 (1 2)。当我们绘制这个结构时，实际上两次引用的是相同的列表。

Scheme 的列表操作函数

Scheme 提供了一些内置函数来操作列表：

• (list 1 2 3 4)：创建一个包含元素 1 2 3 4 的列表。
• (null? nil)：检查一个列表是否为空，nil 是空列表，因此返回 #t。
• (list? '(1 2 3))：检查一个对象是否是列表，返回 #t。
• (list? 3)：检查 3 是否为列表，返回 #f。

通过这些函数，我们可以灵活操作链表，并实现复杂的数据结构。

符号与引用

在 Scheme 中，引用（quotation）允许我们将符号本身作为值使用，而不是求值其绑定的值。当我们使用单引号（'）来引用某个符号或表达式时，Scheme 将不会对其进行求值，而是将其保留为符号或原始表达式本身。这种机制在 Lisp 家族的语言中非常重要，因为它使得编程语言可以轻松地将程序代码本身作为数据进行处理。

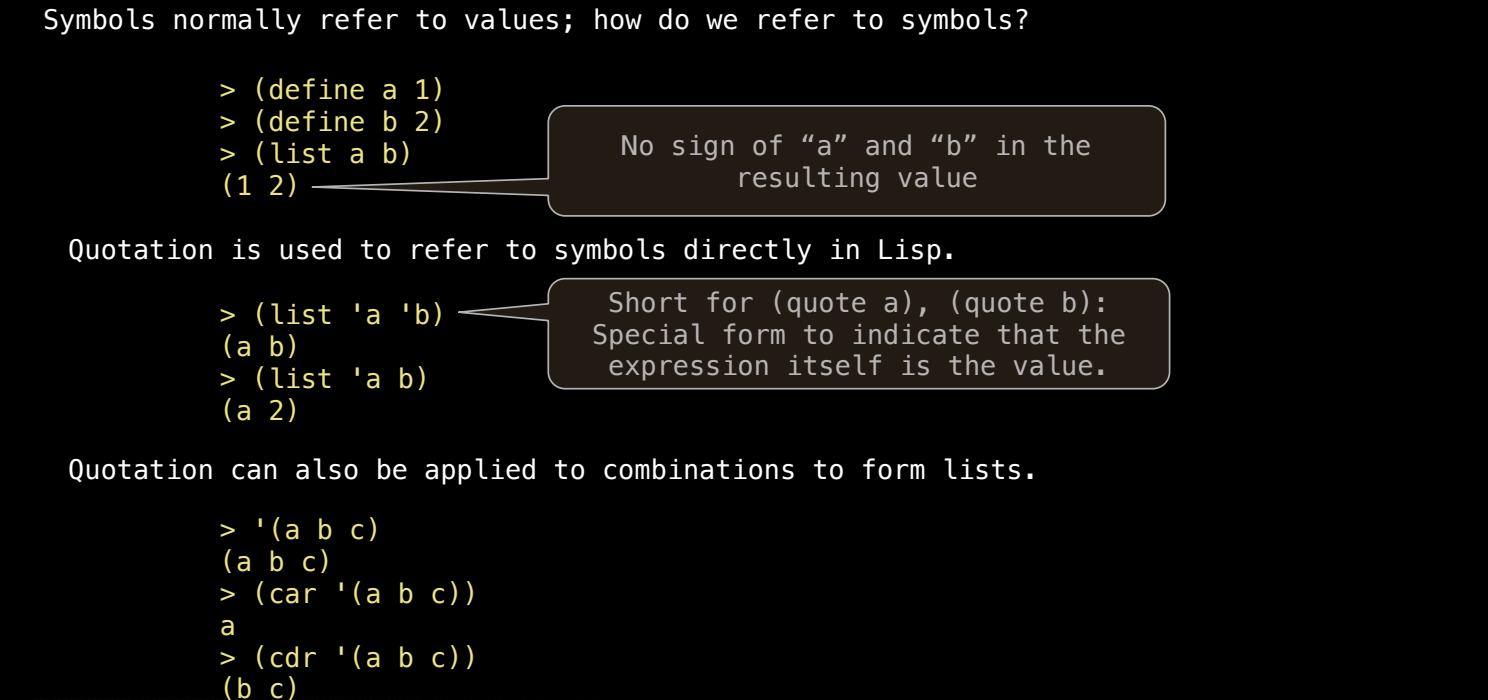
引用符号和表达式

当我们引用符号时，它们不会被求值。例如，假设我们有以下代码：

(define a 1)
(define b 2)

如果我们创建一个包含 a 和 b 的列表，而不使用引号，那么 Scheme 会将它们求值为 1 和 2：

(list a b)  ; 返回 (1 2)

然而，如果我们使用引号引用符号 a 和 b，那么它们将不会被求值，而是保留为符号本身：

(list 'a 'b)  ; 返回 (a b)

这意味着 a 和 b 在列表中是符号，而不是它们绑定的值。

引用实际上是 quote 特殊形式的简写，单引号是 quote 的语法糖。例如，'a 相当于 (quote a)。因此，以下两种写法是等价的：

(list 'a 'b)
(list (quote a) (quote b))

引用组合表达式

我们不仅可以引用符号，还可以引用整个组合表达式。例如，引用 (a b c) 将创建一个包含符号 a、b 和 c 的列表，而不是尝试对它们进行求值：

'(a b c)  ; 返回 (a b c)

在这种情况下，car 操作将返回 a，而 cdr 操作将返回 (b c)。

Programs as Data

eval 过程

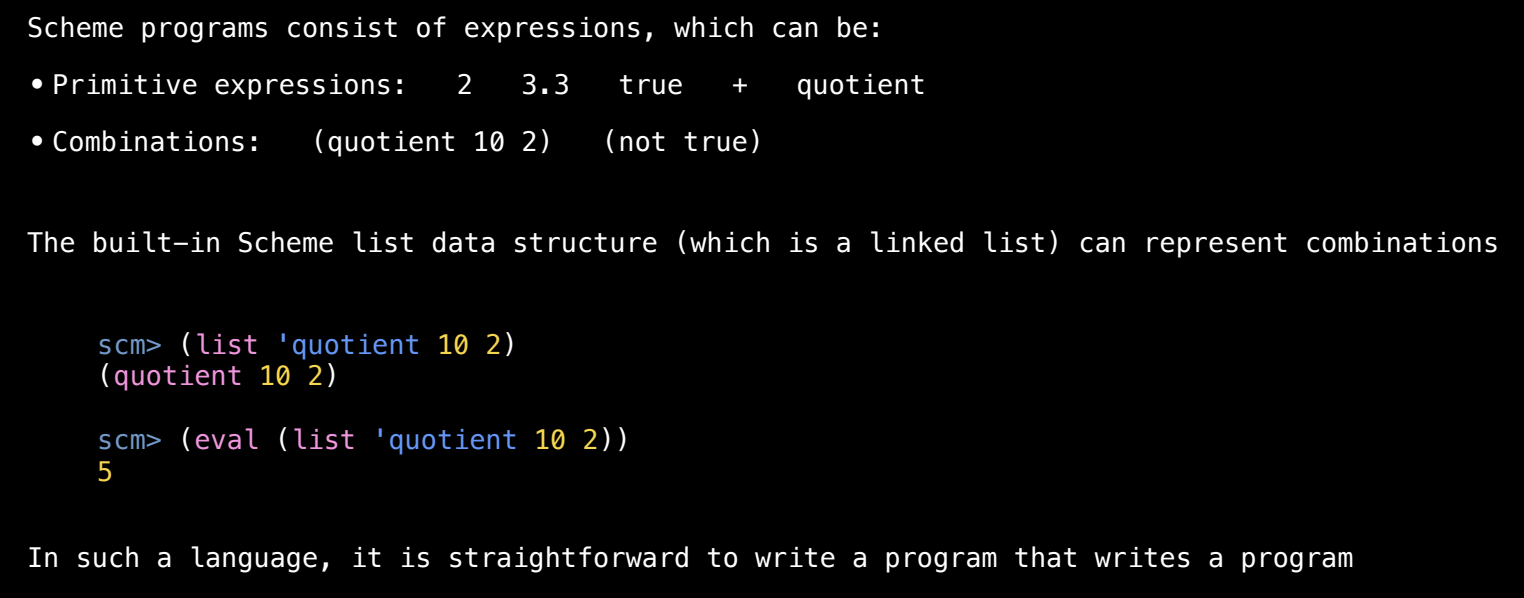
eval 是一个内置过程，它可以对表示为列表的 Scheme 代码进行求值。例如，如果我们创建了一个表示代码的列表：

(list 'quotient 10 2)  ; 返回 (quotient 10 2)

这是一个 Scheme 程序片段，表示 “计算 10 除以 2”。但此时它仅仅是一个列表，没有被执行。如果我们希望执行这个表达式，可以使用 eval：

(eval (list 'quotient 10 2))  ; 返回 5

eval 接受一个表达式并对其求值，就像这个表达式是直接写在程序中的代码一样。使用 eval 可以动态生成并执行代码。

Scheme 中代码即数据

Scheme 中的一大特点是代码本身也是数据。Scheme 的程序由表达式组成，这些表达式可以是原始表达式（如数字、符号）或组合表达式（列表）。因为 Scheme 程序中的代码本质上就是列表，所以处理代码如同处理数据一样自然。例如，构建一个简单的 Scheme 表达式，如计算商：

(list 'quotient 10 2)  ; 返回 (quotient 10 2)

这个表达式本质上是一个列表，包含了符号 quotient 和两个数字 10 和 2。通过 eval，我们可以执行这个表达式。

生成代码的程序

在 Scheme 中，生成代码的程序非常直观，因为代码就是列表。通过操作列表，我们可以动态生成程序片段并使用 eval 执行它们。例如，我们可以编写一个程序，动态生成一个表达式，然后对其求值：

(define expr (list '+ 1 2))  ; 创建表达式 (+ 1 2)
(eval expr)  ; 返回 3

这里，expr 是一个表示加法的列表，通过 eval，我们可以执行这个加法操作并得到结果。

阶乘的递归定义

在 Scheme 中，我们可以使用递归定义来计算数值，比如阶乘或斐波那契数列。此外，Scheme 还提供了一种强大的工具，允许程序生成表达式，这些表达式可以动态地构建和求值。这些特性使 Scheme 特别适合于编写生成其他程序的程序。

首先，我们可以定义一个简单的阶乘递归过程 fact：

(define (fact n)
  (if (= n 0)
      1
      (* n (fact (- n 1)))))

这个 fact 过程遵循经典的递归定义：如果 n 为 0，返回 1，否则返回 n 乘以 fact(n - 1)。调用 fact 5，会得到 5 * 4 * 3 * 2 * 1 = 120。

生成表达式的阶乘

除了返回具体的数值外，我们还可以编写一个返回计算阶乘所需的表达式的过程。这个过程名为 fact-exp，它构建一个组合表达式，而不是返回具体的数值：

(define (fact-exp n)
  (if (= n 0)
      1
      (list '* n (fact-exp (- n 1)))))

这个过程返回的是表示阶乘运算的组合表达式。例如，(fact-exp 5) 会返回表达式 (* 5 (* 4 (* 3 (* 2 (* 1 1)))))。这只是一个表示计算的表达式，而不是立即进行计算。我们可以使用 eval 来对这个表达式求值：

(eval (fact-exp 5))  ; 返回 120

斐波那契数列的递归定义

类似地，我们可以定义斐波那契数列的递归过程：

(define (fib n)
  (if (<= n 1)
      n
      (+ (fib (- n 1)) (fib (- n 2)))))

调用 fib 6 会返回斐波那契数列的第 6 项，结果是 8。这个过程使用树形递归来计算前两项的和。

生成表达式的斐波那契数列

同样地，我们可以编写一个生成斐波那契数列表达式的过程 fib-exp：

(define (fib-exp n)
  (if (<= n 1)
      n
      (list '+ (fib-exp (- n 1)) (fib-exp (- n 2)))))

调用 (fib-exp 6) 会生成一个嵌套的表达式，表示如何计算斐波那契数列的第 6 项。如果我们对该表达式进行求值：

(eval (fib-exp 6))  ; 返回 8

我们会得到斐波那契数列的实际计算结果。

Generating Code

quasi-quote 和 unquote

Scheme 提供了准引用（quasi-quote）功能，使得生成表达式更为灵活。准引用使用反引号（`）表示，它允许我们引用一个表达式，同时可以使用逗号（,）解除某些部分的引用以进行求值。例如：

(define b 4)
`(a ,(+ b 1))  ; 返回 (a 5)

这里，a 是被引用的符号，而 (+ b 1) 通过逗号解除引用并被求值为 5。准引用允许我们轻松混合引用和求值，特别适用于动态生成代码。

动态生成过程的代码

通过准引用，我们可以编写生成代码的过程。例如，生成一个加法过程：

(define (make-add-procedure n)
  `(lambda (d) (+ d ,n)))

调用 (make-add-procedure 2) 会返回一个新的过程，它接收一个参数 d 并返回 d + 2 的结果。使用 eval 可以执行生成的代码：

(define add-2 (eval (make-add-procedure 2)))
(add-2 3)  ; 返回 5

这里，我们生成了一个动态的加法过程，通过传入不同的 n，可以生成不同的加法器。

while 循环示例

在 Scheme 中，虽然没有像 Python 中的 while 循环语句，但我们可以通过递归来实现相同的迭代行为。下面我们将深入探讨如何使用递归和 Scheme 的灵活性，特别是通过生成代码的方式，来模拟类似 while 的行为并解决问题。

在 Python 中，假设我们想计算小于 10 的偶数平方和，代码如下：

x = 2
total = 0
while x < 10:
    total += x ** 2
    x += 2

该程序通过 while 循环不断更新 x 和 total，最终返回 2^2 + 4^2 + 6^2 + 8^2 = 120。

Scheme 中的递归替代

由于 Scheme 没有 while 语句，我们可以通过递归函数来模拟迭代。例如，计算小于 10 的偶数平方和的递归实现如下：

(define (sum-squares x total)
  (if (< x 10)
      (sum-squares (+ x 2) (+ total (* x x)))
      total))

这个递归过程 sum-squares 的逻辑与 while 循环类似：

• 如果 x 小于 10，则递归调用自身，更新 x 和 total。
• 当 x 不再小于 10 时，返回累积的 total。

调用时，初始值 x 为 2，total 为 0：

(sum-squares 2 0)  ; 返回 120

动态生成 while 循环的代码

如果我们希望通过一个通用的函数动态生成类似的递归代码，可以使用 Scheme 的准引用（quasi-quotation）和递归函数生成过程。假设我们想要生成一个可以处理任意初始值、任意条件、任意更新规则和任意累加方式的递归函数。

我们可以编写一个生成递归代码的函数，接受初始值、循环条件、累加规则和更新规则作为参数：

(define (generate-while-expression init-x condition update-x add-to-total)
  `(begin
     (define (loop x total)
       (if ,condition
           (loop ,update-x (+ total ,add-to-total))
           total))
     (loop ,init-x 0)))

在这个函数中：

• 我们使用准引用（`）生成一个 begin 表达式，内含一个递归函数 loop，用于模拟 while 循环。
• condition、update-x 和 add-to-total 通过解除引用（,）动态填充具体的表达式。
• 函数调用 loop 时，初始值 x 和 total 分别设置为 init-x 和 0。

使用示例

1. 计算偶数平方和：

   (eval (generate-while-expression 2 '(< x 10) '(+ x 2) '(* x x)))  ; 返回 120
   

   这个表达式生成的代码等价于：

   (begin
     (define (loop x total)
    (if (< x 10)
        (loop (+ x 2) (+ total (* x x)))
        total))
     (loop 2 0))
   

   然后通过 eval 对生成的表达式进行求值，返回结果 120。

2. 计算平方小于 50 的数的和：

   (eval (generate-while-expression 1 '(< (* x x) 50) '(+ x 1) 'x))  ; 返回 28
   

   这个表达式生成的递归函数计算小于 50 的数的平方和（1^2 + 2^2 + 3^2 + ...），结果为 28。

函数生成代码的能力

通过这种方式，我们可以编写函数来生成其他函数的代码，并动态填充其中的变量。这种能力使得 Scheme 非常强大和灵活，特别是在需要自动化生成代码的场景中。

准引用与解除引用

在上述过程中，准引用（`）和解除引用（,）的使用尤为关键：

• 准引用用于生成代码框架，表示整个表达式大部分内容是固定的。
• 解除引用允许我们将动态内容嵌入准引用的表达式中，从而使得生成的代码灵活可变。

Scheme 的代码生成能力

Scheme 和 Lisp 语言家族的一大特点是能够生成程序代码。我们可以编写一个程序，它不仅仅执行计算，还可以生成新的代码，再通过 eval 对这些代码进行求值。这种能力使得 Scheme 在编写动态生成代码的工具、编译器、解释器等方面具有独特的优势。

这种编写代码生成器的能力，正是许多开发者选择 Lisp 和 Scheme 的原因之一。它极大地增强了编程语言的表现力，让编写复杂和动态程序更加简洁和自然。