Chapter 1: From Zero to One
《Digital Design and Computer Architecture: RISC-V Edition》
本书的第一章标题为“从零到一”,其核心是引导读者理解计算机系统的基础架构及数字设计的基本原理。章节从最基础的概念入手,逐步揭示了现代计算机系统的工作机制。标题”从零到一”不仅暗示了从数字电路的基本原理到复杂计算机设计的递进过程,也暗指了计算机运算从“0”和“1”这种二进制表示开始的本质。第一章的内容设定为打下坚实的基础,帮助理解复杂的计算机设计。
Chapter 1 :: Topics 第一章主题
本章讨论的主题从最基本的计算概念入手,逐步构建出数字设计的全貌。这些主题不仅涵盖了计算机设计的理论知识,也提供了实际应用中的设计思路。以下是第一章讨论的主要主题:
-
The Art of Managing Complexity (管理复杂性的艺术):在现代数字设计中,设计的复杂性往往是最大的挑战之一。如何有效地管理和应对这些复杂性,成为了计算机架构设计中的关键问题。
- Number Systems (数字系统):计算机运算的基础是不同的数制系统,包括二进制、十六进制等。理解数制及其转换是理解计算机如何处理数据的基础。
- Binary Numbers (二进制数)
- Hexadecimal Numbers (十六进制数)
- Bits, Bytes, Nibbles (位、字节和半字节)
- Addition (加法)
- Signed Numbers (有符号数)
- Extension (扩展)
-
Logic Gates (逻辑门):逻辑门是组成数字电路的基本单元,它们执行简单的逻辑运算。
-
Logic Levels (逻辑电平):逻辑电平是指电路中信号的高低电压状态,表示二进制“0”和“1”。
-
CMOS Transistors (CMOS晶体管):CMOS技术是现代集成电路设计的基础,了解CMOS晶体管的工作原理对于理解更复杂的电路设计至关重要。
-
Transistor-Level Gate Design (晶体管级别的门设计):探讨了如何使用晶体管构建逻辑门,这是从硬件层面设计计算机的重要环节。
- Power Consumption (功耗):计算机设计中的一个重要挑战是功耗问题,尤其是在现代移动设备和嵌入式系统中,这一问题尤为突出。
这些主题覆盖了从基础理论到实际设计的各个层面,帮助学生全面理解数字设计的过程。
The Art of Managing Complexity
本节主要探讨了如何应对复杂性的问题。随着计算机设计的规模和复杂性不断增加,设计者面临的最大挑战之一是如何将复杂的系统有效地分解和管理。本节提供了几种方法来帮助设计者管理复杂性。
如何设计超出单人理解范围的系统?
设计一个复杂的计算机系统,通常超出了一个人能够完全理解和掌握的范围。设计者必须依赖抽象工具和方法,将问题分解为可以独立处理的子模块。
-
Abstraction (抽象):抽象是一种关键工具,它允许设计者忽略系统的细节,仅关注其功能行为。例如,在设计逻辑电路时,可以仅考虑输入与输出之间的逻辑关系,而不必关心实现的具体晶体管级别细节。
-
Discipline (规范性):在设计中保持规范性对于管理复杂性至关重要。这意味着使用标准化的设计方法、符号和工具,以确保系统的不同部分能够无缝地集成。
-
The Three –y’s (三种方法):
- Hierarchy (层次化):通过建立层次结构,设计者可以将系统分解为多个子系统,每个子系统可以进一步拆分为更小的模块。
- Modularity (模块化):模块化设计意味着系统的每个子模块都是独立的,可以单独设计、测试和维护。
- Regularity (规则化):规则化强调使用一致的设计模式和架构,减少例外情况的数量。
通过这三种方法,设计者可以逐步简化复杂系统的设计过程,使其更加可控、可维护。
Abstraction (抽象)
在数字设计和计算机架构中,抽象是一种隐藏复杂细节的强大工具,尤其是在这些细节在特定设计阶段不重要的时候。抽象的目标是帮助设计者聚焦于系统的核心功能,避免被低层次的实现细节所干扰。
在课程所涉及的计算机系统中,抽象可以分为多个层次,从最底层的物理现象(如电子运动)到最高层的软件应用程序。每个层次都有其特定的功能与关注点:
- Physics (物理层):物质的基本组成单位,如电子的运动,描述了计算机在物理层面的工作原理。
- Devices (器件层):半导体器件,如晶体管和二极管,用来构建基本的电路组件。
- Analog Circuits (模拟电路):放大器和滤波器等电路,用于信号处理。
- Digital Circuits (数字电路):处理离散信号,包含与非门、或非门等逻辑门。
- Logic (逻辑层):处理逻辑运算的电路,如加法器和存储器,执行计算和存储数据。
- Micro-architecture (微架构):描述了处理器的内部结构,如数据通路、控制器等。
- Architecture (架构层):定义了计算机系统的结构,如指令集架构(RISC-V),确定了处理器如何与内存和I/O设备交互。
- Operating Systems (操作系统):作为底层软件,管理硬件资源,并为应用程序提供接口。
- Application Software (应用软件):最终层次,执行如设备驱动和用户程序的操作。
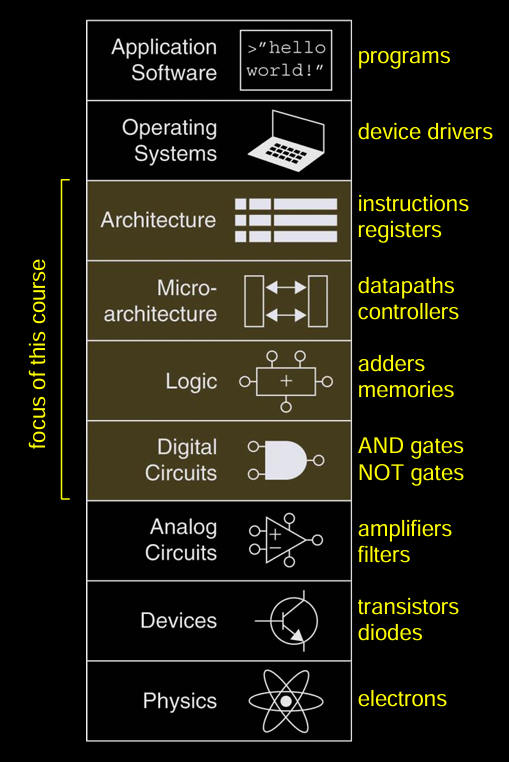
本课程的关注点是从架构层到逻辑与数字电路层次。抽象允许设计者只需关心这些层次的功能和行为,而无需深入了解底层的物理和器件实现。
Discipline (规范性)
规范性在数字设计中起到了限制设计选择的作用,以简化和统一系统的设计和实现。在这里,规范性体现在数字设计的多个方面。例如:
-
数字规范性 (Digital Discipline):数字设计相比于模拟电路设计更简单,因为它仅涉及离散电压而非连续信号。通过仅使用离散的高低电压(如逻辑0和逻辑1),数字系统的设计和实现变得更为直观和可控。
数字系统的另一个优势是能够构建更复杂和先进的系统,远超模拟系统的能力。这是因为数字系统可以方便地进行编程、扩展和集成。例如,现代数字相机、数字电视、手机和CD等设备都取代了其模拟前身,成为了数字技术的代表性应用。
因此,规范性不仅帮助设计者简化了设计过程,还通过限制和标准化设计选择,确保了系统的可扩展性和可靠性。
The Three –y’s (三种设计方法)
在管理复杂性时,三种设计原则(Hierarchy、Modularity和Regularity)是非常重要的工具:
-
Hierarchy (层次化):层次化设计使得系统可以分解为多个层次,每个层次包含不同的功能模块。通过引入层次结构,设计者可以将一个复杂的系统分解为多个易于理解和管理的子系统。
-
Modularity (模块化):模块化设计允许系统的各个部分独立设计、开发和测试。模块化系统中的每个模块可以独立执行特定任务,模块之间的相互作用通过标准化的接口进行。这种方式提高了系统的可维护性和可扩展性,并允许不同团队并行开发。
-
Regularity (规则化):规则化是通过减少设计中的特殊情况和不规则结构来简化系统。规则化设计不仅使系统更易于设计和实现,还提高了系统的可重复性和可维护性。
通过这三种方法,设计者可以将复杂的系统构建得更加模块化、规范化,从而简化设计过程,并增强系统的可扩展性和复用性。
Example: Model T Ford (实例:T型福特车)
T型福特车是数字设计中的经典例子,展示了通过模块化、层次化和规则化的设计原则,如何将复杂系统简化为易于管理的模块化部分。这种设计思路不仅在汽车工业中得到了广泛应用,也在现代计算机和数字系统设计中占据重要地位。
Interchangeable Parts (可互换零件)
T型福特车的革命性贡献之一是引入了可互换零件的概念。与早期由技工手工打造的汽车不同,T型福特车通过流水线的大规模生产大大降低了成本。
在此之前,汽车零件都是手工制造,因此每个零件都可能稍有不同,维修和更换零件需要高技术的技工。福特通过标准化零件的设计,确保了零件在不同车辆间的互换性,这一创新显著提高了生产效率并降低了制造成本。
亨利·福特的愿景:
我将为大众制造一辆汽车,它足够大,可以容纳一个家庭,但又足够小,方便个人驾驶和保养。它将用最好的材料和最优秀的工匠,以最简单的设计制成。而且它将价格低廉,任何有良好收入的人都可以买得起,并在上帝创造的广阔天地中享受与家人在一起的快乐时光。
这段话体现了福特的设计理念:通过简单化设计和批量生产,使汽车成为大众可负担的产品。这种理念在现代数字设计中也十分重要,通过降低复杂性和提高效率,使复杂系统得以更广泛地应用。
Hierarchy (层次化)
T型福特车的设计展示了层次化的思想,即将复杂系统分解为多个子系统,每个子系统进一步分解为更小的组件:
- 汽车的总体结构包括车架、车轮、座椅、发动机等。
- 发动机的组成:发动机包含多个部分,如气缸、火花塞、排气管、化油器等。
- 化油器的构造:化油器又分为多个子组件,如进气口、进气针、供油管、连接螺母等。
通过层次化设计,复杂的汽车系统被分解为多个简单的模块,每个模块负责具体的功能。这种方式不仅简化了生产和维护过程,还使设计、调试和优化更加便捷。
Modularity (模块化)
T型福特车的模块化设计进一步体现在每个组件独立执行特定的功能,并且这些组件可以容易地拆卸和更换。例如:
- 连接螺母的功能:
- 固定燃油管和进气管的接头。
- 防止燃油泄漏。
- 容易拆卸和更换。
每个模块有自己明确的功能,设计者可以独立处理和优化这些模块,而不必考虑整个系统的复杂性。这种设计不仅提高了生产效率,还降低了维修和更换零件的难度。
- 连接螺母的接口:
- 标准化的直径、螺纹节距和扭矩。
通过标准化接口,福特车的零件可以从多个供应商处采购,这种模块化设计极大地增强了零件的兼容性和生产的灵活性。
Regularity (规则化)
T型福特车的另一个重要设计原则是规则化,即通过标准化设计来减少复杂性。所有的T型车使用标准化零件,使得零件之间可以互换,维修和生产成本大大降低。
- 可互换零件:所有标准化的螺母、螺栓、轴承等都可以在不同的车之间互换,这意味着不需要为每辆车定制不同的零件。
福特通过这种规则化设计,确保了生产线的高效运转。正如亨利·福特所说的那句名言:
“任何客户都可以选择自己喜欢的汽车颜色,只要它是黑色的。”
这一句幽默的表达方式实际上突出了规则化设计带来的生产效率和成本优势。在数字系统设计中,规则化的应用同样重要,它确保了系统设计的统一性和简化了生产过程。
通过这些设计原则,福特车不仅在汽车工业中创造了历史,也为现代工程设计树立了重要的基准。这些原则同样适用于数字设计领域,在计算机架构中,通过层次化、模块化和规则化的设计,可以极大地简化系统的复杂性并提高其效率和可维护性。
The Digital Abstraction (数字抽象)
在物理世界中,大多数物理量是连续的。例如:
- 电压:导线上的电压通常是一个连续变化的值,可以在某个范围内变化。
- 振荡频率:振荡器的频率也可能是连续的,可以有任意的变化范围。
- 质量的位置:物体的位置是一个连续变量,理论上可以处于任意位置。
然而,在数字系统中,这些连续变量通过数字抽象被简化为离散值的子集。数字抽象将复杂的、连续的物理世界转化为更简单的离散模型。在该模型中,物理现象只被认为是两个或多个离散状态,通常是“高”或“低”电压对应“1”或“0”二进制值。这种抽象的力量在于,它大大简化了计算机系统的设计、分析和实现,使得复杂系统得以更高效、可靠地工作。
The Analytical Engine (解析引擎)
解析引擎是查尔斯·巴贝奇(Charles Babbage)于1834年到1871年之间设计的一种早期计算机,被认为是第一台数字计算机。尽管它没有被最终完成,但它的设计思想为现代计算机奠定了基础。
- 机械齿轮:该引擎通过机械齿轮运作,每个齿轮代表一个离散的值(如0到9)。这与现代计算机中使用的二进制位(0和1)类似,都是对离散值的表示和处理。
- 巴贝奇的设计没有完全实现,他在去世之前没能完成这一项目。然而,解析引擎的基本构造和理念,预示了计算机如何处理和存储数据,成为现代数字系统设计的先驱。
Digital Discipline: Binary Values (数字规范:二进制值)
在数字设计中,系统通过二进制值进行信息处理,二进制值的使用是数字设计的核心规范之一。具体来说,二进制系统仅使用两种离散值来表示信息:
- 1和0:数字系统中的两种基本状态,分别对应“高”电压和“低”电压。
- 1可以表示为TRUE或HIGH,而0则表示FALSE或LOW。
- 电压级别:在数字电路中,电压被用于表示这些离散的二进制值。
- 低电压(通常接地,GND)代表0。
- 高电压(例如电源电压,VDD)代表1。
通过这种二进制电压的表示方式,复杂的计算和数据处理可以通过简单的电压切换来实现,这也是数字系统高效运行的基础。二进制的简单性大大简化了系统设计,使其比模拟电路更易于实现和扩展。
- Bit (比特):在二进制系统中,最小的信息单位称为比特(bit),每个比特可以表示为0或1。比特是所有数字信息的基本组成部分,复杂的信息和数据处理均可以通过比特的组合来完成。
Number Systems: Binary Numbers
数制系统:二进制数
在计算机设计和架构中,数制系统是最基础的概念之一。现代数字系统的核心是二进制数,而理解数制系统,特别是二进制数制,是理解计算机如何进行数据处理的关键。
Decimal Numbers (十进制数)
十进制数是我们日常生活中最常用的数制系统。它以基数10为基础,由0到9共十个数字组成。每个数字的位置表示不同的幂次。例如,数字5374可以表示为:
\[ 5374_{10} = 5 \times 10^3 + 3 \times 10^2 + 7 \times 10^1 + 4 \times 10^0 \]
在这个例子中:
- 5位于千位(\(10^3\)),代表5000;
- 3位于百位(\(10^2\)),代表300;
- 7位于十位(\(10^1\)),代表70;
- 4位于个位(\(10^0\)),代表4。
这种表示方法利用了位置值来表示不同的幂次,这是所有数制系统的共通特点。
Binary Numbers (二进制数)
二进制数是数字系统的基础,它仅使用0和1两个符号表示数字。二进制与十进制类似,每个数字的位置也表示不同的幂次,但二进制以基数2为基础。例如,二进制数1101可以表示为:
\[1101_2 = 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 8 + 4 + 0 + 1 = 13_{10}\]在这个例子中:
- 最左边的1位于2的三次幂(\(2^3\))的位置,表示8;
- 第二个1位于\(2^2\)的位置,表示4;
- 第三个0位于\(2^1\)的位置,表示0;
- 最右边的1位于\(2^0\)的位置,表示1。
二进制数的简单性使其在硬件实现中极为高效,尤其是在电路设计中,因为它只需要区分两种状态:高电压和低电压。
Counting in Binary (二进制计数)
二进制的计数方式类似于十进制,但每位只能是0或1。当最低位达到1后,它向高位进位。例如:
| Binary (二进制) | Decimal (十进制) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
通过这种逐位进位的方式,二进制数可以表示任意大的整数。
Powers of Two (二的幂次)
在二进制数中,2的幂是非常重要的概念,因为每一位二进制数都与2的某个幂次相关。理解并记住常用的2的幂次,对于数字设计和计算机体系结构的学习非常有帮助。以下是一些常见的2的幂次:
- \( 2^0 = 1 \)
- \( 2^1 = 2 \)
- \( 2^2 = 4 \)
- \( 2^3 = 8 \)
- \( 2^4 = 16 \)
- \( 2^5 = 32 \)
- \( 2^6 = 64 \)
- \( 2^7 = 128 \)
- \( 2^8 = 256 \)
- \( 2^9 = 512 \)
- \( 2^{10} = 1024 \)
- \( 2^{11} = 2048 \)
- \( 2^{12} = 4096 \)
- \( 2^{13} = 8192 \)
- \( 2^{14} = 16384 \)
- \( 2^{15} = 32768 \)
这些幂次经常出现在计算机的存储和数据处理过程中。例如,计算机的存储容量通常以千字节(\(2^{10}\))或兆字节(\(2^{20}\))来衡量。掌握这些幂次可以帮助我们快速理解系统中数值的规模。
Number Conversion (数制转换)
数制转换在计算机系统中是非常基础的技能。计算机内部使用二进制数,而我们日常使用的是十进制数,因此了解如何在这两种数制之间进行转换非常重要。
Binary to Decimal Conversion (二进制转十进制)
将二进制数转换为十进制数的过程是将二进制数的每一位乘以其对应的2的幂次,然后将结果相加。例如,转换二进制数 10011₂ 为十进制数:
\[ 10011_2 = 1 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 \]
\[ = 16 + 0 + 0 + 2 + 1 = 19_{10} \]
因此,10011₂ 等于 19₁₀。
Decimal to Binary Conversion (十进制转二进制)
将十进制数转换为二进制数可以通过多种方法实现。这里介绍两种常用的方法:
Method 1: Subtraction Method (减法法)
- 找到小于或等于该十进制数的最大2的幂次。
- 用该2的幂次的值从十进制数中减去。
- 重复上述步骤,直到结果为0。
例如,将 47₁₀ 转换为二进制数:
- 47 大于 \(2^5 = 32\),因此 47 - 32 = 15,保留 1 在 \(2^5\) 位置。
- 15 大于 \(2^3 = 8\),因此 15 - 8 = 7,保留 1 在 \(2^3\) 位置。
- 7 大于 \(2^2 = 4\),因此 7 - 4 = 3,保留 1 在 \(2^2\) 位置。
- 3 大于 \(2^1 = 2\),因此 3 - 2 = 1,保留 1 在 \(2^1\) 位置。
- 1 等于 \(2^0 = 1\),因此 1 - 1 = 0,保留 1 在 \(2^0\) 位置。
因此,47₁₀ 等于 101111₂。
Method 2: Division Method (除法法)
- 将十进制数连续除以2,记录每次除以2得到的余数。
- 继续除到商为0为止。
- 将所有余数逆序排列。
例如,将 47₁₀ 转换为二进制数:
- 47 ÷ 2 = 23,余数 1
- 23 ÷ 2 = 11,余数 1
- 11 ÷ 2 = 5,余数 1
- 5 ÷ 2 = 2,余数 1
- 2 ÷ 2 = 1,余数 0
- 1 ÷ 2 = 0,余数 1
逆序排列余数,结果为 101111₂。
Binary Values and Range (二进制数的取值范围)
对于任何数制,不同位数的数字可以表示不同数量的值,且范围也随位数增加而变化。
- N-digit decimal number (N位十进制数):
- 十进制数中,N位数可以表示的值的数量为 \(10^N\),范围为0到 \(10^N - 1\)。
- 例如,一个三位的十进制数可以表示从 000 到 999 的值,共有1000个值。
- N-bit binary number (N位二进制数):
- 二进制数中,N位数可以表示的值的数量为 \(2^N\),范围为0到 \(2^N - 1\)。
- 例如,一个三位的二进制数可以表示从 000₂ 到 111₂ 的值,即0到7,共有8个值。
理解位数与范围的关系在计算机设计中非常重要,因为它影响了存储器的容量、数据的表示能力以及硬件设计的规模。
Number Systems: Hexadecimal Numbers
数制系统:十六进制数
十六进制数是数字系统中常用的数制之一,特别是在处理计算机系统和数字电路时。与二进制数相比,十六进制数可以更紧凑地表示相同的值,因此常用于简化二进制数的表示和读写。
Hexadecimal Numbers (十六进制数)
- Base 16 (基数16):十六进制以16为基数,使用数字0到9和字母A到F来表示16个不同的数值。字母A到F分别表示十进制的10到15。
- Shorthand for Binary (二进制的简写):十六进制数实际上是二进制数的简写。每个十六进制数位可以直接映射为四位二进制数位(称为一个半字节或Nibble),这使得在十六进制和二进制之间的转换非常方便。
十六进制、十进制和二进制的等价表
| Hex Digit (十六进制) | Decimal Equivalent (十进制) | Binary Equivalent (二进制) |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
Hexadecimal to Binary Conversion (十六进制到二进制的转换)
将十六进制数转换为二进制数非常简单,因为每个十六进制数位直接映射为四位二进制数。例如,转换十六进制数 4AF₁₆(或写作 0x4AF)为二进制数:
- 将每个十六进制数位分别转换为对应的四位二进制数:
- 4₁₆ = 0100₂
- A₁₆ = 1010₂
- F₁₆ = 1111₂
- 将这些二进制数组合在一起: \[ 4AF₁₆ = 0100 1010 1111₂ \]
因此,4AF₁₆ 等于 0100 1010 1111₂。
Hexadecimal to Decimal Conversion (十六进制到十进制的转换)
将十六进制数转换为十进制数的步骤与二进制到十进制的转换类似,使用权重将每个位置上的数值乘以16的相应幂次,然后求和。例如,转换 4AF₁₆ 为十进制数:
- 从最右边开始,每个位置的数值乘以16的幂次:
- F₁₆ = 15,所以 15 × \(16^0\) = 15
- A₁₆ = 10,所以 10 × \(16^1\) = 160
- 4₁₆ = 4,所以 4 × \(16^2\) = 1024
- 将这些结果相加: \[ 4AF₁₆ = 1024 + 160 + 15 = 1199₁₀ \]
因此,4AF₁₆ 等于 1199₁₀。
Hexadecimal and Binary Prefixes (十六进制与二进制前缀)
在编写文本文件或代码时,使用下标标注数制(如₁₆或₂)有时不便,因此很多编程语言采用了前缀表示法来区分不同的数制。
- Hexadecimal (十六进制) 使用前缀
0x来表示:- 例如,
0x23AB表示十六进制数 23AB₁₆。
- 例如,
- Binary (二进制) 使用前缀
0b来表示:- 例如,
0b1101表示二进制数 1101₂。
- 例如,
这种表示方式使得数制转换更加清晰,特别是在需要同时处理二进制和十六进制的编程环境中。
Number Systems: Bytes, Nibbles, & All That Jazz
数制系统:字节、半字节及相关概念
在计算机系统中,位、字节和半字节是表示和处理数据的基础单位。
Bits, Bytes, Nibbles (位、字节和半字节)
- Byte (字节):由 8位 (bits) 组成,代表 \(2^8 = 256\) 种不同的数值。
- Nibble (半字节):由 4位 (bits) 组成,代表 \(2^4 = 16\) 种不同的数值。
- 一个字节由两个半字节组成,一个半字节正好能表示一个十六进制数位(Hex Digit)。
每一位(bit)表示二进制中的一个0或1。一个十六进制数位由4位二进制表示,因此两个十六进制数位组成一个字节(8位二进制数)。
例子
-
10010110₂:这是一个8位的二进制数,表示一个字节。最左边的是最高有效位(Most Significant Bit,MSB),最右边的是最低有效位(Least Significant Bit,LSB)。
-
CEBF9AD7₁₆:这是一个由4个字节(32位)组成的十六进制数,每个字节可以通过两个十六进制数位表示。

Large Powers of Two (二的高次幂)
在计算机存储和数据处理领域,2的幂次是非常常见的。这是因为计算机使用二进制系统,基于2的幂次来计算存储容量、处理能力和其他关键性能指标。
- \( 2^{10} = 1 \text{ kilo} \approx 10^3 \) (1024)
- \( 2^{20} = 1 \text{ mega} \approx 10^6 \) (1,048,576)
- \( 2^{30} = 1 \text{ giga} \approx 10^9 \) (1,073,741,824)
- \( 2^{40} = 1 \text{ tera} \approx 10^{12} \)
- \( 2^{50} = 1 \text{ peta} \approx 10^{15} \)
- \( 2^{60} = 1 \text{ exa} \approx 10^{18} \)
这些幂次常用于衡量数据存储(如千字节、兆字节、千兆字节等)以及处理能力的大小。
Number Systems: Addition
数制系统:加法
在数字系统中,理解如何进行加法运算是至关重要的,不论是在十进制还是二进制中,加法的基本规则都是相同的:从最低位开始相加,遇到进位则将进位加到下一位。计算机系统中的加法操作依赖于二进制数,因此了解二进制加法是学习计算机架构的基础。
Decimal Addition (十进制加法)
在十进制加法中,每一列从右到左相加,若结果超过9,则进位到下一列。例如:
\[ 3734 + 5168 = 8902 \]
在计算过程中:
- 从个位开始:4 + 8 = 12,写下2,进1。
- 十位:3 + 6 = 9,加上进位的1得到10,写下0,进1。
- 百位:7 + 1 = 8,加上进位的1得到9,写下9。
- 千位:3 + 5 = 8,写下8。
加法结果为 8902,并且每次进位都标注在上方。
Binary Addition (二进制加法)
二进制加法与十进制加法类似,不同之处在于二进制只有两个数字:0和1。二进制加法的规则如下:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10(即0,进1)
例如,计算:
\[ 1011₂ + 0011₂ = 1110₂ \]
步骤如下:
- 最低位:1 + 1 = 10,写下0,进1。
- 第二位:1 + 1 = 10,加上进位的1,得到11,写下1,进1。
- 第三位:0 + 0 = 0,加上进位的1,得到1。
- 第四位:1 + 0 = 1,没有进位。
结果为 1110₂。
Binary Addition Examples (二进制加法示例)
示例1
计算以下两个4位二进制数的加法:
\[ 1001₂ + 0101₂ \]
- 最低位:1 + 1 = 10,写下0,进1。
- 第二位:0 + 0 = 0,加上进位的1,得到1。
- 第三位:0 + 1 = 1。
- 第四位:1 + 0 = 1。
结果为 1110₂。
示例2
计算以下两个4位二进制数的加法:
\[ 1011₂ + 0110₂ \]
- 最低位:1 + 0 = 1。
- 第二位:1 + 1 = 10,写下0,进1。
- 第三位:0 + 1 = 1,加上进位的1,得到10,写下0,进1。
- 第四位:1 + 0 = 1,加上进位的1,得到10,写下0,进1。
结果为 10001₂,溢出了5位。
Overflow (溢出)
溢出 是数字系统中的一个重要概念。计算机在固定位数的基础上进行运算,当计算结果超出了可用位数的表示范围时,就会产生溢出。例如,假设一个系统只能处理4位二进制数:
- 当计算 11₂ + 6₂ (即 1011₂ + 0110₂)时,结果为 10001₂,但该系统只能存储4位,因此会发生溢出,计算结果会错误地变为 0001₂。
溢出在计算机系统中会引发数据错误或不可预期的行为,因此在设计时必须考虑如何处理溢出。
Number Systems: Signed Numbers
数制系统:有符号数
在计算机系统中,处理正负数是非常重要的。有符号数是表示正负数的二进制数,通过增加一个符号位 (Sign Bit) 来区分正数和负数。常见的两种表示方法是符号/绝对值表示法 (Sign/Magnitude) 和二进制补码表示法 (Two’s Complement)。
Signed Binary Numbers (有符号二进制数)
有符号二进制数主要有两种表示方法:
- Sign/Magnitude Numbers (符号/绝对值表示法):使用一个符号位表示正负,剩余位表示数值的大小。
- Two’s Complement Numbers (二进制补码表示法):通过特殊的补码规则来表示负数,这种方法能够简化运算,广泛用于现代计算机中。
Sign/Magnitude Numbers (符号/绝对值表示法)
- 使用 1个符号位 和 N-1个绝对值位。
- 符号位是最高有效位(最左边的位),表示数值的正负:
- 符号位为 0 表示正数。
- 符号位为 1 表示负数。
4位符号/绝对值表示法的例子
- +6:表示为 0110
- -6:表示为 1110
在这种表示法中,数值部分不变,仅符号位决定正负号。使用N位的符号/绝对值数的表示范围为 \(- (2^{N-1}-1)\) 到 \(+ (2^{N-1}-1)\),因此,4位数的表示范围是 \(-7\) 到 \(+7\)。
Problems with Sign/Magnitude Numbers (符号/绝对值表示法的问题)
- 加法不适用:符号/绝对值表示法存在运算问题,特别是在进行加法运算时。例如,计算 \(-6 + 6\):
- -6:1110
- +6:0110
- 相加得到:10100,这是错误的结果,因为它超出了4位数的表示范围。
- 零的双重表示:在符号/绝对值表示法中,零可以有两种表示方式,即正零和负零:
- 0000 表示 +0
- 1000 表示 -0
这种冗余表示在计算中会导致不一致和混淆。
Two’s Complement Numbers (二进制补码)
二进制补码 (Two’s Complement) 是现代计算机中处理有符号数的标准方法。与符号/绝对值表示法 (Sign/Magnitude) 相比,二进制补码解决了运算中的加法问题,并确保零只有一种表示形式。
Why Use Two’s Complement? (为何使用二进制补码?)
- Addition works: 在二进制补码中,加法运算不需要特殊处理正负数,正数和负数可以直接相加。
- Single representation for 0: 二进制补码中的零只有一种表示形式,避免了符号/绝对值表示法中“+0”和“-0”的问题。
Two’s Complement Representation (二进制补码表示法)
在N位的二进制补码表示中:
- 最高有效位 (MSB) 的权重是 \(-2^{N-1}\)。
- 其余位的权重按标准二进制表示递增,即 \(2^0, 2^1, …, 2^{N-2}\)。
例如,4位二进制补码数可以表示的范围是:
- 最正的数:\(0111_2\) = 7₁₀
- 最负的数:\(1000_2\) = -8₁₀
4位二进制补码的表示范围是 \(-8\) 到 \(+7\)。
Reversing the Sign (反转符号)
要反转一个二进制补码数的符号,可以通过以下步骤完成:
- 取反所有位(即0变1,1变0)。
- 加1。
Example (例子)
将二进制数 3₁₀ = 0011₂ 反转符号:
- 取反:0011₂ → 1100₂
- 加1:1100₂ + 1 = 1101₂
因此,反转后的结果是 1101₂,表示 -3₁₀。
Two’s Complement Examples (二进制补码示例)
示例1:反转 6₁₀ 的符号
将十进制数 6₁₀ = 0110₂ 反转符号:
- 取反:0110₂ → 1001₂
- 加1:1001₂ + 1 = 1010₂
反转符号后的结果是 1010₂,表示 -6₁₀。
示例2:二进制补码数 1001₂ 的十进制值是多少?
因此,二进制补码数 1001₂ 表示的是 -7₁₀。
Two’s Complement Addition (二进制补码加法)
在二进制补码中,加法运算与无符号数加法的规则相同。由于二进制补码能够表示负数,因此可以直接对正负数进行加法运算,而无需考虑符号位的特殊处理。
Example 1: 6 + (-6)
我们将 6 和 -6 表示为二进制补码:
- 6₁₀ = 0110₂
- -6₁₀ = 1010₂
相加: \[ 0110₂ + 1010₂ = 0000₂ \] 结果为 0000₂,即 0₁₀,没有溢出,这是正确的结果。
Example 2: -2 + 3
我们将 -2 和 3 表示为二进制补码:
- -2₁₀ = 1110₂
- 3₁₀ = 0011₂
相加: \[ 1110₂ + 0011₂ = 0001₂ \] 结果为 0001₂,即 1₁₀。
Subtraction (二进制补码减法)
在二进制补码中,减法可以通过将减数的符号反转(取补码)然后进行加法运算来实现。这与加法操作一致,简化了硬件设计。
Example: 3 - 5
将减法转化为加法,即 3 + (-5):
- 3₁₀ = 0011₂
- -5₁₀ = 1011₂
相加: \[ 0011₂ + 1011₂ = 1110₂ \] 结果为 1110₂,即 -2₁₀。
Number System Comparison (数制系统比较)
不同的数制系统有不同的数值表示范围。以下是常见数制系统的范围对比:
| Number System | Range |
|---|---|
| Unsigned (无符号数) | \([0, 2^N - 1]\) |
| Sign/Magnitude (符号/绝对值) | \([-(2^{N-1}-1), 2^{N-1}-1]\) |
| Two’s Complement (二进制补码) | \([-2^{N-1}, 2^{N-1}-1]\) |
4位数的例子
- 无符号数:从 0000₂ 到 1111₂,对应的十进制范围为 0 到 15。
- 符号/绝对值:从 1000₂ (-0) 到 0111₂ (+7),范围为 -7 到 +7。
- 二进制补码:从 1000₂ (-8) 到 0111₂ (+7),范围为 -8 到 +7。
二进制补码的表示法不仅解决了加法和减法中的问题,还提供了更广泛的负数表示能力,尤其是在处理硬件运算时具有重要优势。

Number Systems: Extension
数制系统:扩展
当我们需要在数字系统中将一个数的位宽从 \(N\) 扩展到 \(M\)(即增加位数,且 \(M > N\))时,有两种常见的方法:符号扩展 (Sign-extension) 和 零扩展 (Zero-extension)。这些方法用于确保数值在增加位宽的过程中仍然保持正确。
Increasing Bit Width (增加位宽)
- Sign-extension (符号扩展):适用于二进制补码数,用于扩展有符号数。
- Zero-extension (零扩展):适用于无符号数,用于扩展无符号数。
Sign-Extension (符号扩展)
符号扩展通过将符号位复制到扩展位来保持数值不变。该方法适用于二进制补码数,这样可以确保数值的符号和大小在扩展后保持一致。
- 符号位被复制到新的最高有效位(MSB)。
- 数值保持不变。
Example 1
- 4位数 3₁₀ = 0011₂。
- 扩展为8位:将符号位(0)复制到前面四位,结果为 00000011₂。
Example 2
- 4位数 -5₁₀ = 1011₂。
- 扩展为8位:将符号位(1)复制到前面四位,结果为 11111011₂。
Zero-Extension (零扩展)
零扩展通过在扩展位中填充零来增加位宽。这种方法适用于无符号数,但在处理负数时,数值会发生变化,因为符号信息会丢失。
- 在扩展位填充零。
- 对于负数,数值会改变,因为符号位不再保留。
Example 1
- 4位无符号数 3₁₀ = 0011₂。
- 扩展为8位:在前面四位填充零,结果为 00000011₂,值保持不变。
Example 2
- 4位数 -5₁₀ = 1011₂(此时表示负数)。
- 扩展为8位:在前面四位填充零,结果为 00001011₂,但此时值变为 11₁₀,与原来的值不同。
Logic Gates
逻辑门
逻辑门是数字电路的基础组件,它们用于执行基本的逻辑运算。通过将输入信号转换为输出信号,逻辑门帮助实现复杂的计算功能。不同类型的逻辑门具有不同的逻辑功能,常见的逻辑门包括 NOT、AND、OR、NAND、NOR、XOR、XNOR 等。
Types of Logic Gates (逻辑门类型)
-
Single-input gates (单输入逻辑门):这些逻辑门只有一个输入信号。例如,NOT门(反相器)和BUF门(缓冲器)。
-
Two-input gates (双输入逻辑门):有两个输入信号,常见的双输入逻辑门有 AND、OR、XOR、NAND、NOR、XNOR。
-
Multiple-input gates (多输入逻辑门):逻辑门可以接受多个输入,处理复杂的逻辑运算。
Single-Input Logic Gates (单输入逻辑门)
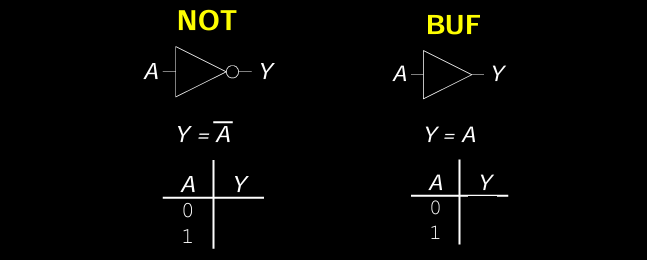
- NOT Gate (非门):
- 逻辑功能:将输入信号取反。
- 真值表:
A Y 0 1 1 0 - 逻辑表达式:\( Y = \overline{A} \)
-
Buffer (缓冲器):
- 逻辑功能:直接输出与输入相同的值。
- 真值表:
A Y 0 0 1 1 - 逻辑表达式:\( Y = A \)
Two-Input Logic Gates (双输入逻辑门)
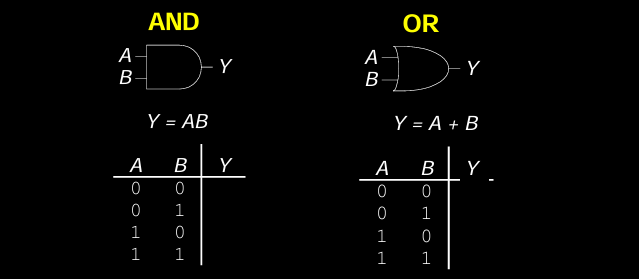
- AND Gate (与门):
- 逻辑功能:仅当两个输入都为1时,输出为1,否则为0。
- 真值表:
A B Y 0 0 0 0 1 0 1 0 0 1 1 1 - 逻辑表达式:\( Y = A \cdot B \)
- OR Gate (或门):
- 逻辑功能:只要其中一个输入为1,输出为1。
- 真值表:
A B Y 0 0 0 0 1 1 1 0 1 1 1 1 - 逻辑表达式:\( Y = A + B \)
通过这些逻辑门,可以实现更复杂的运算和功能,这些是数字系统和计算机硬件设计的基础。在实际应用中,逻辑门被组合成更复杂的逻辑电路,用于执行诸如加法、比较和存储等基本操作。
More Two-Input Logic Gates (更多双输入逻辑门)
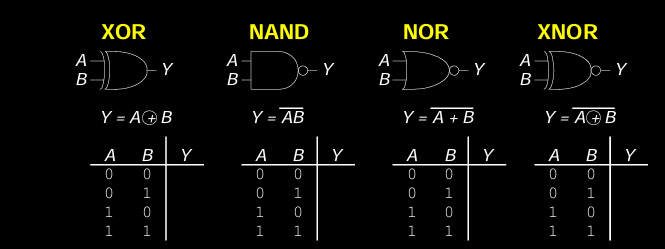
除了基础的 AND 和 OR 门,数字系统还广泛使用其他功能的双输入逻辑门,如 XOR、NAND、NOR 和 XNOR。
- XOR Gate (异或门):
- 逻辑功能:仅当两个输入不同,输出为1。
- 真值表:
A B Y 0 0 0 0 1 1 1 0 1 1 1 0 - 逻辑表达式:\( Y = A \oplus B \)
- NAND Gate (与非门):
- 逻辑功能:与门的反向,两个输入都为1时输出为0,其他情况输出为1。
- 真值表:
A B Y 0 0 1 0 1 1 1 0 1 1 1 0 - 逻辑表达式:\( Y = \overline{A \cdot B} \)
- NOR Gate (或非门):
- 逻辑功能:或门的反向,两个输入都为0时输出为1,其他情况输出为0。
- 真值表:
A B Y 0 0 1 0 1 0 1 0 0 1 1 0 - 逻辑表达式:\( Y = \overline{A + B} \)
- XNOR Gate (同或门):
- 逻辑功能:XOR 门的反向,两个输入相同时输出为1。
- 真值表:
A B Y 0 0 1 0 1 0 1 0 0 1 1 1 - 逻辑表达式:\( Y = \overline{A \oplus B} \)
Multiple-Input Logic Gates (多输入逻辑门)
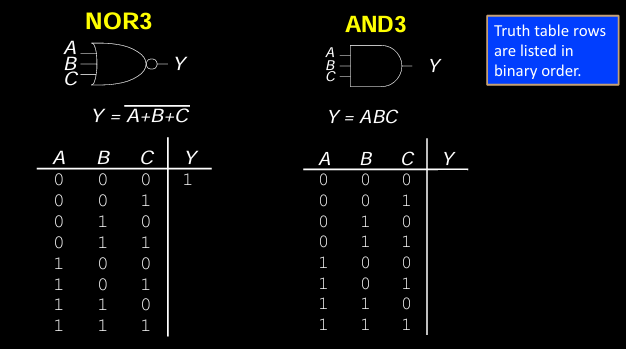
多输入逻辑门处理多个输入信号,常用于复杂的逻辑运算。
- NOR3 Gate (三输入或非门):
- 逻辑功能:只在所有输入都为0时输出1,其他情况下输出0。
- 逻辑表达式:\( Y = \overline{A + B + C} \)
- 真值表(部分):
A B C Y 0 0 0 1 0 0 1 0 1 1 1 0 - AND3 Gate (三输入与门):
- 逻辑功能:所有输入都为1时输出1,否则输出0。
- 逻辑表达式:\( Y = A \cdot B \cdot C \)
- 真值表(部分):
A B C Y 0 0 0 0 1 1 1 1
多输入的 XOR 门常用于计算奇偶校验,因为它可以检测输入的位数中有多少位为1,输出奇偶结果。
SystemVerilog Description (SystemVerilog 逻辑描述)
在硬件描述语言 SystemVerilog 中,逻辑门可以通过模块化的方式进行定义。如下所示的代码描述了不同的逻辑门操作:
module gates(input logic a, b, c,
output logic y1, y2, y3, y4, y5);
not g1(y1, a);
and g2(y2, a, b);
or g3(y3, a, b, c);
nand g4(y4, b, c);
xor g5(y5, a, c);
endmodule
- g1 定义了 NOT 门。
- g2 定义了 AND 门。
- g3 定义了 OR 门,接受三个输入。
- g4 定义了 NAND 门。
- g5 定义了 XOR 门。
George Boole, 1815–1864 (乔治·布尔)
乔治·布尔是逻辑代数的奠基人,他的贡献对现代计算机科学产生了深远的影响:
- 他出身于工人阶级家庭,自学成才,后来成为爱尔兰女王学院的数学教授。
- 1854年,他出版了《思维法则研究》(An Investigation of the Laws of Thought),这本书确立了逻辑代数的基础。
- 他引入了二进制变量的概念,并提出了三种基本的逻辑运算:AND、OR、NOT。
布尔的工作为后来二进制数字系统的发展铺平了道路,成为数字电路和计算机逻辑设计的基石。
在 Verilog 和 Chisel 中,都可以描述逻辑门和电路功能,但它们的使用方式和语法略有不同。Verilog 是一种广泛使用的硬件描述语言(HDL),而 Chisel 是基于 Scala 的一种硬件设计语言,更多地借助高级编程语言的特性来生成硬件描述。
1. Verilog 中的逻辑描述
在 Verilog 中,逻辑门可以通过模块(
module)来定义,也可以通过布尔表达式直接描述逻辑。下面是一些基本逻辑门的 Verilog 描述示例:Verilog Example
module logic_gates ( input wire a, b, c, output wire y_not, y_and, y_or, y_nand, y_xor ); // 定义逻辑门 not (y_not, a); // NOT 门 and (y_and, a, b); // AND 门 or (y_or, a, b, c); // OR 门(多个输入) nand (y_nand, a, b); // NAND 门 xor (y_xor, a, c); // XOR 门 endmodule
- 在此代码中,每个逻辑门通过 Verilog 内置的原语(如
not、and、or、nand、xor)实现。- 输入
a、b、c被用于不同的逻辑门运算,结果通过输出y_not、y_and等信号得到。布尔表达式的 Verilog 描述
module logic_gates_bool ( input wire a, b, c, output wire y ); assign y = (a & b) | (~a & c); // 布尔表达式定义逻辑 endmodule
assign语句用来定义一个布尔表达式,该表达式实现了逻辑组合功能。&是按位 AND,|是按位 OR,~是按位 NOT。2. Chisel 中的逻辑描述
在 Chisel 中,逻辑门通过布尔操作符实现,Chisel 是一种嵌入式 DSL,使用 Scala 编写。每个信号都是
Bool类型,逻辑操作通过 Scala 操作符来描述。Chisel Example
import chisel3._ class LogicGates extends Module { val io = IO(new Bundle { val a = Input(Bool()) val b = Input(Bool()) val c = Input(Bool()) val y_not = Output(Bool()) val y_and = Output(Bool()) val y_or = Output(Bool()) val y_nand = Output(Bool()) val y_xor = Output(Bool()) }) // 定义逻辑门 io.y_not := ~io.a // NOT 门 io.y_and := io.a & io.b // AND 门 io.y_or := io.a | io.b | io.c// OR 门(多个输入) io.y_nand := ~(io.a & io.b) // NAND 门 io.y_xor := io.a ^ io.c // XOR 门 }
- 输入
io.a、io.b、io.c是输入信号,io.y_not、io.y_and等是输出信号。- 逻辑运算通过 Scala 的操作符实现:
~用于 NOT,&用于 AND,|用于 OR,^用于 XOR。- Chisel 使用 Scala 的 DSL 特性来简洁表达硬件逻辑,与 Verilog 类似的功能可以通过更简短的代码来实现。
使用布尔表达式的 Chisel 描述
import chisel3._ class LogicGatesBool extends Module { val io = IO(new Bundle { val a = Input(Bool()) val b = Input(Bool()) val c = Input(Bool()) val y = Output(Bool()) }) // 使用布尔表达式来定义逻辑 io.y := (io.a & io.b) | (~io.a & io.c) }
- 这里的布尔表达式与 Verilog 中的
assign类似,使用了 Scala 的逻辑运算符。Verilog 和 Chisel 的对比
特点 Verilog Chisel 语言类型 硬件描述语言 (HDL) 硬件设计语言 (HDL/DSL) 语法风格 类似 C 语言的硬件描述风格 基于 Scala 的函数式编程风格 硬件逻辑描述 使用内置的原语( and、or等)使用 Scala 操作符和 DSL 表达式 可扩展性 限于 HDL 语法 高度可扩展,支持参数化、生成器模式 综合效率 已广泛应用于硬件设计,成熟且稳定 生成 Verilog 后与现有工具链兼容
- Verilog 更适合传统硬件设计,语法接近硬件电路实现,较为低级,适合直接描述寄存器传输级别(RTL)的设计。
- Chisel 提供了更高级的抽象,利用函数式编程和参数化生成器来提高硬件设计的灵活性和可重用性。Chisel 可以生成 Verilog 代码,用于传统的硬件综合工具链。
两者都可以用于描述逻辑门和更复杂的数字电路,选择哪一种取决于设计需求、开发习惯和项目规模。
Verilog 和 SystemVerilog 都是用于硬件描述的语言(HDL),但它们之间存在重要的区别。SystemVerilog 是 Verilog 的扩展和增强版本,旨在提高设计和验证的效率。SystemVerilog 不仅继承了 Verilog 的功能,还引入了许多新的语法和特性,尤其在硬件验证方面有显著的增强。
1. Verilog 简介
Verilog 是一种硬件描述语言(HDL),于 1985 年开发,用于描述数字电路和系统。Verilog 的主要功能是帮助设计者在寄存器传输级(RTL)层面描述硬件结构,并通过综合工具将这些设计转化为实际的硬件实现。它常用于设计数字电路,例如处理器、存储器、和 FPGA(现场可编程门阵列)等。
Verilog 的主要特点
- 硬件设计:适用于硬件结构的描述,支持组合逻辑、时序逻辑、状态机等。
- 低级别描述:主要用于描述寄存器传输级(RTL)的设计,强调硬件的实现细节。
- 模块化设计:使用模块 (
module) 定义硬件组件。- 有限的验证能力:Verilog 提供基本的测试平台,但验证功能有限,适合小规模设计。
2. SystemVerilog 简介
SystemVerilog 是对 Verilog 的扩展,最初于 2002 年由 Accellera 标准组织发布,并于 2005 年成为 IEEE 标准(IEEE 1800)。它是在 Verilog 的基础上添加了大量的新特性,特别是强化了验证功能,提供了先进的建模和验证功能,使其成为一种强大的硬件设计和验证语言。
SystemVerilog 的增强特性
- 支持面向对象的编程 (OOP):引入了类(
class)、继承、封装、多态等面向对象编程的概念,用于设计复杂的验证环境。- 更强大的数据类型:增加了新的数据类型,如
logic(避免 Verilog 中reg和wire的混淆)和bit,使得建模更加灵活和准确。- 高级验证特性:引入了诸如断言(assertions)、随机化、约束、覆盖率驱动的验证(coverage-driven verification, CDV)等验证功能,支持 UVM(通用验证方法学)。
- 接口(interfaces):SystemVerilog 支持
interface,用来简化模块间的信号连接和处理,大大简化了复杂硬件系统的设计。- 模块化设计增强:增强了
module的功能,引入了package、interface等高级模块化特性,有助于代码的重用和组织。- 静态和动态并存:支持静态硬件描述与动态仿真验证,适用于硬件和测试平台的同时描述。
3. Verilog 与 SystemVerilog 的关系
SystemVerilog 是 Verilog 的超集,意味着 SystemVerilog 兼容所有 Verilog 的语法和特性。因此,Verilog 代码可以在 SystemVerilog 环境中直接使用,但 SystemVerilog 提供了更多强大的功能来改进设计和验证。
总结:Verilog 是 SystemVerilog 的基础,SystemVerilog 作为 Verilog 的扩展,涵盖了 Verilog 的所有特性,并增加了更多高级功能,特别是验证和面向对象编程方面。
4. Verilog 与 SystemVerilog 的主要区别
特性 Verilog SystemVerilog 开发年代 1985 2002(扩展),2005(标准化) 设计能力 专注于硬件描述(RTL 设计) 硬件设计 + 强大的验证功能 面向对象编程 不支持 支持(类、继承、多态、封装等) 数据类型 reg、wire新增 logic、bit、byte等模块化设计 基于 module,无interface支持 module、interface和package验证功能 验证功能较弱,主要依赖手写的测试台 支持断言、随机化、约束和覆盖率驱动的验证 断言(Assertions) 不支持 原生支持,用于设计和验证断言 随机化 不支持 原生支持,支持随机测试生成 覆盖率驱动验证 (CDV) 不支持 支持,通过 covergroup提供覆盖率跟踪功能接口 (Interfaces) 不支持 支持,通过 interface来简化模块间连接枚举类型 不支持 支持, enum类型可用队列 (Queues) 不支持 支持动态数组和队列,适用于仿真和验证 工具支持 广泛支持,各大EDA工具均支持 与 Verilog 相同,现代工具全面支持 SystemVerilog 5. SystemVerilog 关键特性详解
1. 面向对象编程(OOP)
SystemVerilog 允许使用面向对象的特性,这极大地增强了其在验证方面的灵活性。通过类 (
class),可以创建复杂的测试环境,如仿真验证中的事务、驱动器、监控器等组件。class MyClass; int x; function new(int value); x = value; endfunction endclass2. 断言 (Assertions)
SystemVerilog 支持断言,用于在设计和验证中验证某些条件是否成立。这对于捕捉仿真中的错误非常有用。
assert (a == b) else $error("a and b are not equal");3. 接口 (Interfaces)
interface提供了一种方式来简化模块之间的连接,特别是在信号较多的情况下。它能够把多个信号打包,并通过modport控制方向。interface myInterface; logic a, b, c; modport in (input a, b); modport out (output c); endinterface4. 随机化与约束 (Randomization and Constraints)
SystemVerilog 提供内置的随机化功能,用于创建随机的输入场景,并通过约束来控制随机值的生成范围和条件。
class MyRandomClass; rand int x; constraint c { x > 0 && x < 100; } endclass
Logic Levels
逻辑电平
逻辑电平表示数字电路中的电压值,用于区分逻辑0和逻辑1。在实际的数字系统中,离散的电压代表逻辑信号中的“1”和“0”。
1. Discrete Voltages Represent 1 and 0 (离散电压表示1和0)
- 逻辑 0 通常表示为接地电压(GND),即 0伏。
- 逻辑 1 通常表示为电源电压(\(V_{DD}\)),例如 5伏。
示例
- 0伏表示逻辑 0,而5伏表示逻辑 1。
- 但如果电压不是刚好5伏或0伏,比如 4.99伏 或 3.2伏,则如何判断该电压是逻辑0还是逻辑1?
2. Range of Voltages (电压范围)
实际上,逻辑系统并不会要求精确的0伏或5伏,而是为逻辑0和逻辑1定义了电压范围。这些范围允许一定的噪声或其他电气干扰:
- 逻辑 0 的电压范围可能是 0伏 到某个阈值(如 0.8伏)。
- 逻辑 1 的电压范围可能是从某个阈值(如 2伏或 3.5伏)到 \(V_{DD}\)。
每个数字电路都有为输入和输出电压设置的容许范围,这样可以允许一定的噪声干扰,而不会影响正常的逻辑判断。
3. Logic Levels for Inputs and Outputs (输入输出的逻辑电平)
为了允许噪声,输入和输出信号的逻辑电平有不同的电压范围:
- 输入电平 可能比输出电平更宽松,因为电路要允许外部信号带有一定的干扰。
- 输出电平 则尽量保证电压值的稳定,以提供更可靠的逻辑值。
What is Noise? (什么是噪声?)
噪声是指任何会降低信号质量的现象,这种干扰可能源自多种物理因素,包括:
- 电阻:导线的电阻会导致信号电压下降,特别是在长距离传输中。
- 电源噪声:电源中的波动或不稳定性会影响电路中的电压水平。
- 耦合效应:临近的导线之间的电磁干扰也会造成信号的劣化。
Noise Example (噪声示例)
假设某个驱动器(driver)输出5伏的逻辑1信号,但由于传输线的电阻,接收器(receiver)只接收到 4.5伏。尽管这是一个接近5伏的信号,但仍然可能受到噪声的影响。在这种情况下,4.5伏仍然被认为是逻辑1,但噪声降低了信号的质量。
- 驱动器输出:5V
- 接收器接收到:4.5V
这表明噪声可以改变信号的实际电平,因此,数字电路设计中必须考虑噪声的影响,确保信号在噪声干扰下仍然可以正确识别。
The Static Discipline (静态纪律)
静态纪律是一种硬件设计原则,用于确保数字电路中的每个组件在接受到有效的逻辑输入时,能够生成有效的逻辑输出。这一原则规定了如何使用特定范围的电压值来表示离散的逻辑信号,即逻辑“1”和逻辑“0”。
- 逻辑有效输入:输入的电压值必须在预定的逻辑高电平或逻辑低电平范围内。
- 逻辑有效输出:输出的电压值也必须符合特定的逻辑电平要求。
限定电压范围 (Limited Voltage Ranges)
为了保证电路的可靠性,使用有限的电压范围来代表离散值。在输入和输出的逻辑电平范围内,电路元件必须处理和传递这些信号,确保数字系统的稳定性。
Noise Margins (噪声裕量)
噪声裕量是硬件设计中的一个重要概念,用来衡量电路对噪声的抗干扰能力。它定义了输出和输入之间的电压余量,允许信号在传播过程中受到一定的干扰或降解,但仍能被正确识别为逻辑“1”或逻辑“0”。
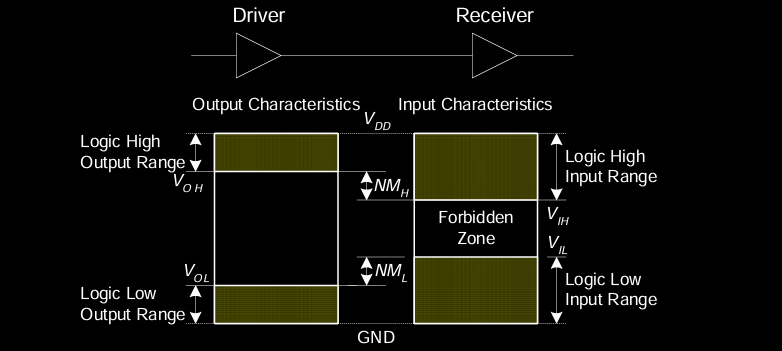
逻辑电平范围
- 逻辑高电平输出范围 (\(V_{OH}\)):驱动器输出的电压范围,用于表示逻辑“1”。
- 逻辑低电平输出范围 (\(V_{OL}\)):驱动器输出的电压范围,用于表示逻辑“0”。
- 逻辑高电平输入范围 (\(V_{IH}\)):接收器接受的电压范围,能正确识别为逻辑“1”。
- 逻辑低电平输入范围 (\(V_{IL}\)):接收器接受的电压范围,能正确识别为逻辑“0”。
噪声裕量定义
- 高电平噪声裕量 (\(NM_H\)):逻辑高电平下,允许的噪声幅度,即 \( NM_H = V_{OH} - V_{IH} \)。
- 低电平噪声裕量 (\(NM_L\)):逻辑低电平下,允许的噪声幅度,即 \( NM_L = V_{IL} - V_{OL} \)。
Noise Example (噪声示例)
在实际的信号传输中,噪声可能会影响驱动器输出的信号。例如,驱动器输出5伏表示逻辑“1”,但由于导线电阻或其他因素,接收器可能只接收到4.5伏。在这种情况下,4.5伏仍然在接收器的逻辑高输入范围内,因此信号依然被正确识别为逻辑“1”。
DC Transfer Characteristics (直流传输特性)
DC传输特性描述了数字电路中信号的电压传输行为,特别是当输入电压逐渐从低电平(0V)变化到高电平(\(V_{DD}\))时,输出电压的响应情况。
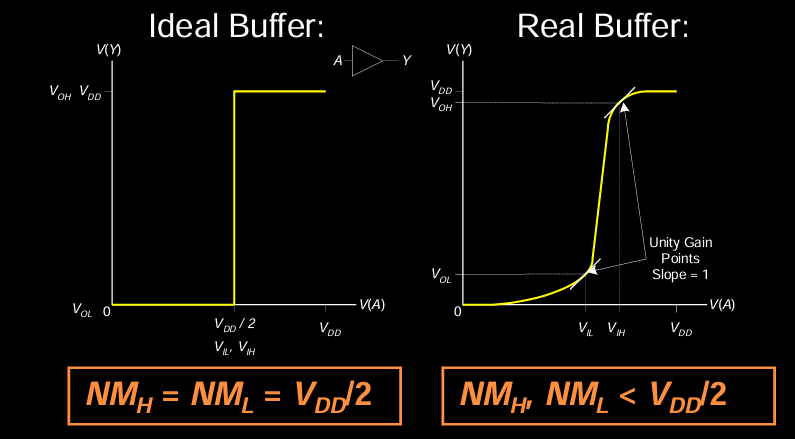
理想缓冲器 (Ideal Buffer)
在理想条件下,缓冲器的输出会完美对应输入电压的变化:
- 输入电压从0逐渐升高到\(V_{DD}\),在中间会出现突变,输出从0跳变到\(V_{DD}\),即完美的逻辑电平转换。
- 噪声裕量在理想条件下是对称的,\(NM_H = NM_L = V_{DD}/2\)。
实际缓冲器 (Real Buffer)
在现实中,由于器件的非理想特性,缓冲器的传输特性会有一些偏差:
- 随着输入电压变化,输出电压的变化不再是理想的突变,而是渐变的。
- 实际缓冲器的噪声裕量较小,通常 \(NM_H\) 和 \(NM_L\) 都小于 \(V_{DD}/2\),且不完全对称。
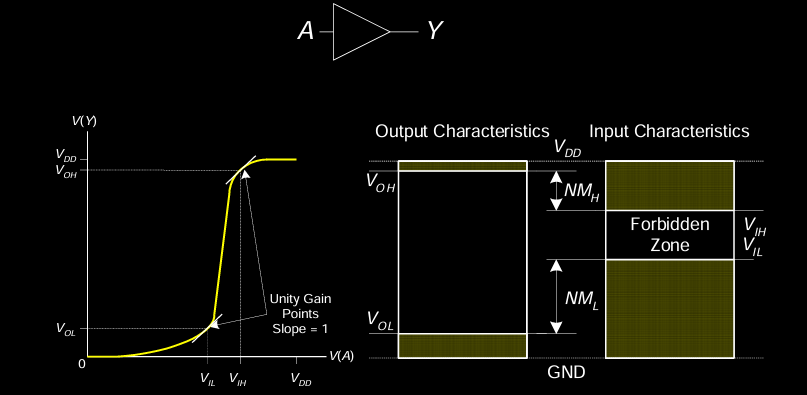
理想缓冲器 (Ideal Buffer)
在理想情况下:
- 当输入电压从低电平(\(0V\))上升时,输出电压会迅速从低电平(\(V_{OL}\))跳变到高电平(\(V_{OH}\)),这种跳变是非常迅速且没有中间过渡的。
- 输入电压 \(V_A\) 在中点 \(V_{DD}/2\) 时,输出发生突变。
实际缓冲器 (Real Buffer)
在实际电路中:
- 缓冲器的输入输出特性并不完全理想,输出电压会在输入电压逐渐升高时慢慢从 \(V_{OL}\) 上升到 \(V_{OH}\)。
- 实际传输特性会显示出一种平滑的斜坡,输入电压经过一段模糊区域(称为增益区域)时,输出会逐渐变化。
- 噪声裕量 (\(NM_H\) 和 \(NM_L\)) 通常小于理想情况,且可能不对称。
噪声裕量公式
- 理想情况:\( NM_H = NM_L = V_{DD}/2 \)
- 实际情况:\( NM_H, NM_L < V_{DD}/2 \),并且在实际电路中可能不完全相等。
VDD Scaling (电源电压缩放)
VDD 缩放指的是随着时间推移,电路使用的电源电压逐渐降低。过去,数字电路的标准电源电压为 5V,但由于工艺改进和功耗考虑,现代电路中电源电压已经降低。
电压缩放历史
- 在 1970s 和 1980s,大多数数字电路使用的电源电压 \(V_{DD}\) 为 5V。
- 现在,随着工艺尺寸缩小和更小、更节能的晶体管的使用,标准电压逐渐降低到 3.3V、2.5V、1.8V、1.5V、1.2V、1.0V 等。
电压缩放的原因
- 防止晶体管烧毁:随着工艺节点的缩小,较高的电压会给微小的晶体管带来更大的压力,可能导致它们烧毁。
- 降低功耗:降低 \(V_{DD}\) 可以减少功耗,这在移动设备和节能应用中尤为重要。
电压缩放的注意事项
- 不同电压级的芯片连接时需要特别小心,避免因电压不匹配导致损坏或功能异常。
Logic Family Examples (逻辑系列示例)
不同的逻辑家族使用不同的电源电压和逻辑电平阈值。常见逻辑家族及其对应的输入、输出电平如下表:
| 逻辑家族 | \(V_{DD}\) 电源电压 | \(V_{IL}\) 低输入电平 | \(V_{IH}\) 高输入电平 | \(V_{OL}\) 低输出电平 | \(V_{OH}\) 高输出电平 |
|---|---|---|---|---|---|
| TTL | 5V (4.75 - 5.25) | 0.8V | 2.0V | 0.4V | 2.4V |
| CMOS | 5V (4.5 - 6) | 1.35V | 3.15V | 0.33V | 3.84V |
| LVTTL | 3.3V (3 - 3.6) | 0.8V | 2.0V | 0.4V | 2.4V |
| LVCMOS | 3.3V (3 - 3.6) | 0.9V | 1.8V | 0.36V | 2.7V |
逻辑家族说明
- TTL (Transistor-Transistor Logic):经典的晶体管-晶体管逻辑电路,常用于早期的数字电路设计。
- CMOS (Complementary Metal-Oxide-Semiconductor):广泛应用的现代低功耗逻辑电路。
- LVTTL (Low-Voltage TTL):低电压版本的 TTL,常用于现代低功耗设备。
- LVCMOS (Low-Voltage CMOS):低电压 CMOS,与 LVTTL 类似,适用于低功耗应用。
这些逻辑家族的不同特性决定了它们在不同应用中的使用场景。设计人员需要根据具体应用的电压和噪声要求选择合适的逻辑家族。
CMOS Transistors
CMOS晶体管
晶体管 是现代数字电路的基础,逻辑门由晶体管构建。最常用的晶体管技术是 CMOS(互补金属氧化物半导体),其主要构件是 nMOS 和 pMOS 晶体管。每个晶体管都可看作是一个三端口的电压控制开关,其通断状态由第三个端口(栅极)电压控制。
晶体管的工作原理
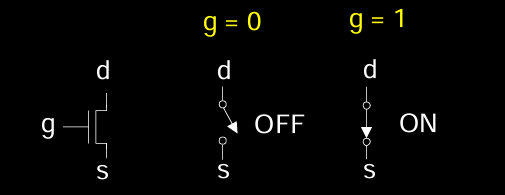
- 三端口开关:晶体管有三个端口,分别是 d(漏极)、s(源极)、g(栅极)。
- 电压控制:当 g = 1 时,晶体管导通,d 和 s 连接;当 g = 0 时,晶体管断开,d 和 s 断开。
- 晶体管的这两个状态对应逻辑门的“1”和“0”输出,借助多个晶体管组合,可以实现复杂的逻辑功能。
工作状态
- g = 0 时:开关为断开状态,晶体管处于 OFF 状态,d 和 s 不导通。
- g = 1 时:开关为闭合状态,晶体管处于 ON 状态,d 和 s 导通。
Robert Noyce (罗伯特·诺伊斯)
罗伯特·诺伊斯是电子行业的重要人物之一,被誉为“硅谷市长”(Mayor of Silicon Valley)。他在半导体工业和集成电路的发明方面作出了重要贡献。
- Fairchild半导体公司:1957年,诺伊斯共同创立了Fairchild Semiconductor,这家公司推动了半导体技术的快速发展。
- Intel公司:1968年,诺伊斯共同创立了英特尔公司(Intel),后来成为全球最大的半导体芯片制造商之一。
- 集成电路的发明者之一:诺伊斯参与了集成电路(IC)的发明,集成电路使得现代计算机和电子设备的小型化和高效化成为可能。
Silicon (硅)
硅 是制作晶体管的主要材料,硅是一种半导体,其导电能力介于导体和绝缘体之间。
硅的特性
- 纯硅 是一个不好的导体,因为其没有自由电荷载体(即不含自由电子或空穴)。
- 通过掺杂过程,可以将硅的导电性大幅提高,使其能够作为半导体使用。
掺杂类型
- n型硅(n-Type Silicon):掺杂了五价元素(如砷As),这类元素引入了额外的自由电子,因此n型硅具有自由电子作为电荷载体,表现为负电荷。
- 自由电子是移动的负电荷载体。
- p型硅(p-Type Silicon):掺杂了三价元素(如硼B),这类元素引入了“空穴”(即缺少电子的位置),因此p型硅具有自由空穴作为电荷载体,表现为正电荷。
- 空穴是移动的正电荷载体。
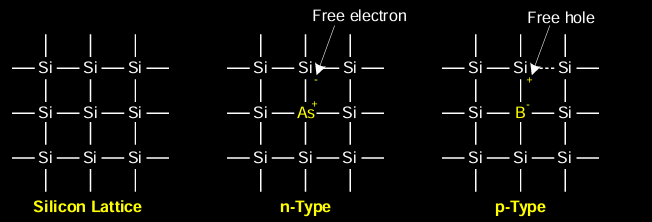
硅的结构
- 硅晶格:由硅原子组成的规则结构,每个硅原子通过共价键与相邻的硅原子结合。
- n型硅晶格:掺杂了少量的五价元素,如砷(As),这些元素为硅晶格引入自由电子。
- p型硅晶格:掺杂了少量的三价元素,如硼(B),这些元素在硅晶格中形成空穴。
MOS Transistors (MOS晶体管)
MOS晶体管 (Metal-Oxide-Semiconductor Transistors) 是现代数字电路设计的核心器件,常见于CMOS技术中。MOS晶体管基于金属-氧化物-半导体结构,通过控制栅极电压来实现开关操作。MOS晶体管分为nMOS和pMOS两种类型,广泛应用于数字逻辑电路中。
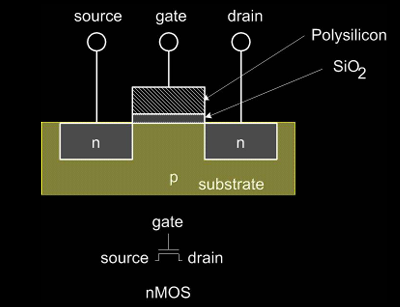
MOS晶体管的组成部分
- 栅极(Gate):控制电流的通断。早期使用金属作为栅极材料,现在一般使用多晶硅(Polysilicon)。
- 氧化层(Oxide):栅极与半导体之间的绝缘层,一般是二氧化硅(\(SiO_2\))。
- 源极和漏极(Source 和 Drain):电流的入口和出口,连接到半导体材料上。
- 掺杂硅(Doped Silicon):通过掺杂不同的元素使硅具有导电性,形成n型和p型半导体。
Transistors: nMOS (nMOS晶体管)
nMOS晶体管的行为可以视为电压控制的开关,其导通和关闭状态取决于栅极电压。
- Gate = 0:当栅极电压为 0 时,晶体管关闭,源极和漏极之间没有通路,电流不流动,nMOS处于OFF状态。
- Gate = 1:当栅极电压为 1 时,晶体管打开,源极和漏极之间形成导电通路,电流可以流动,nMOS处于ON状态。
nMOS的工作原理
- 在 Gate = 1 时,nMOS通过在p型衬底中形成一个n型导电通道,使得电流从源极流向漏极。
- 在 Gate = 0 时,没有形成导电通道,因此电流无法通过。
Transistors: pMOS (pMOS晶体管)
pMOS晶体管与nMOS的行为相反,其导通和关闭状态也由栅极电压控制。
- Gate = 0:当栅极电压为 0 时,pMOS晶体管导通,源极和漏极之间有电流通路,pMOS处于ON状态。
- Gate = 1:当栅极电压为 1 时,pMOS晶体管关闭,源极和漏极之间没有通路,pMOS处于OFF状态。
pMOS的工作原理
- 在 Gate = 0 时,pMOS在n型衬底中形成一个p型导电通道,使得电流可以从源极流向漏极。
- 在 Gate = 1 时,通道关闭,电流无法通过。
Transistor Function (晶体管功能总结)
nMOS和pMOS晶体管共同构成了CMOS技术的核心。它们在工作状态上是互补的,使得CMOS电路具有高效、低功耗的优点。
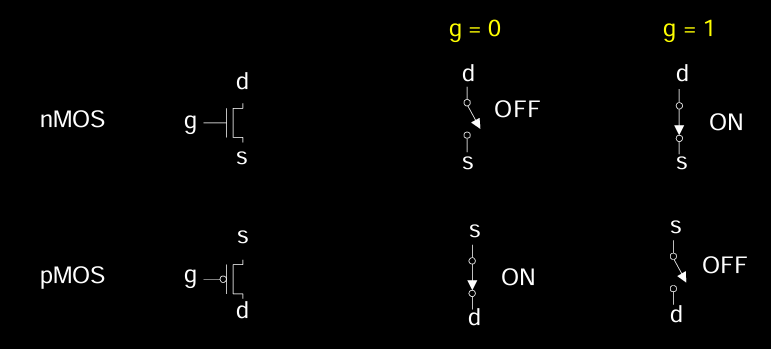
nMOS和pMOS的工作状态对比
- nMOS:
- Gate = 0:关断(OFF),没有导电通道。
- Gate = 1:导通(ON),源极和漏极之间形成导电通道。
- pMOS:
- Gate = 0:导通(ON),源极和漏极之间形成导电通道。
- Gate = 1:关断(OFF),没有导电通道。
通过合理组合nMOS和pMOS,设计者能够实现逻辑电路中常见的逻辑门,如 与非门(NAND)和 或非门(NOR),这些逻辑门是所有现代数字电路的基本构建块。
Transistor Function (晶体管功能)
在CMOS电路中,nMOS和pMOS晶体管的行为是互补的,分别擅长传输逻辑低电平(0)和逻辑高电平(1)。这种互补行为使得CMOS电路具有高效、低功耗的特点。
nMOS 和 pMOS 的功能
- nMOS:擅长传输逻辑低电平(0),因此通常连接源极到 GND(接地)。
- pMOS:擅长传输逻辑高电平(1),因此通常连接源极到 \(V_{DD}\)(电源电压)。
通过将nMOS和pMOS组合使用,可以设计各种逻辑门。CMOS电路的一个基本特性是使用 pull-up 网络和 pull-down 网络共同实现逻辑功能:
- Pull-up网络:由pMOS晶体管组成,用于在需要输出高电平时拉高输出。
- Pull-down网络:由nMOS晶体管组成,用于在需要输出低电平时拉低输出。
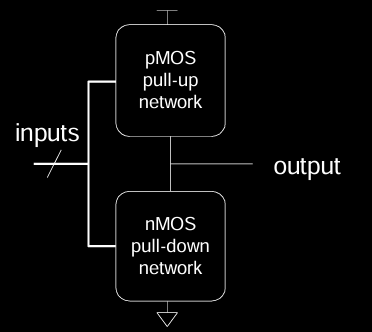
Gates from Transistors
由晶体管实现的逻辑门
通过组合nMOS和pMOS,可以实现各种逻辑门。接下来介绍两种常见的CMOS逻辑门设计:NOT门 和 NAND门。
CMOS Gates: NOT Gate (反相器)
NOT门 或 反相器 是最简单的逻辑门之一,它的功能是将输入信号反转,即当输入为0时,输出为1,反之亦然。
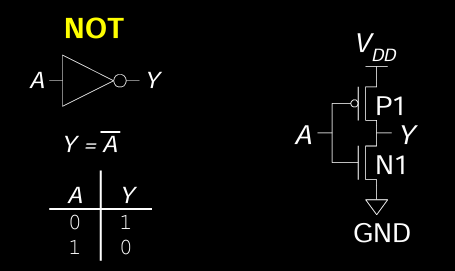
工作原理
- 当 A = 0 时:
- pMOS晶体管(P1)导通(ON),nMOS晶体管(N1)关断(OFF)。
- 输出 Y = 1,被拉高到 \(V_{DD}\)。
- 当 A = 1 时:
- pMOS晶体管(P1)关断(OFF),nMOS晶体管(N1)导通(ON)。
- 输出 Y = 0,被拉低到GND。
真值表
| A | P1 (pMOS) | N1 (nMOS) | Y |
|---|---|---|---|
| 0 | ON | OFF | 1 |
| 1 | OFF | ON | 0 |
CMOS Gates: NAND Gate (与非门)
NAND门 是一种重要的基本逻辑门。它的输出是输入A和B的与操作结果的反(即非与门)。即当两个输入都为1时,输出为0;否则,输出为1。
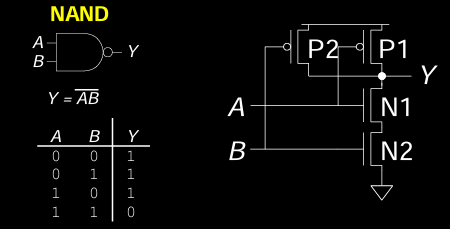
工作原理
- 当 A = 0 或 B = 0 时:
- 至少有一个pMOS晶体管(P1或P2)导通,nMOS晶体管(N1或N2)至少有一个关断,输出 Y = 1,被拉高到 \(V_{DD}\)。
- 当 A = 1 且 B = 1 时:
- pMOS晶体管P1和P2都关断,nMOS晶体管N1和N2都导通,输出 Y = 0,被拉低到GND。
真值表
| A | B | P1 (pMOS) | P2 (pMOS) | N1 (nMOS) | N2 (nMOS) | Y |
|---|---|---|---|---|---|---|
| 0 | 0 | ON | ON | OFF | OFF | 1 |
| 0 | 1 | ON | OFF | OFF | ON | 1 |
| 1 | 0 | OFF | ON | ON | OFF | 1 |
| 1 | 1 | OFF | OFF | ON | ON | 0 |
通过了解nMOS和pMOS晶体管的导通和关断状态,我们可以设计复杂的逻辑门并进行有效的逻辑操作。在CMOS电路中,NAND门是非常重要的构件,它可以组合出其他任意逻辑门。
NOR3 Gate (三输入NOR门)
三输入NOR门 是一个扩展的NOR门,具有三个输入,输出为这三个输入的逻辑“或”运算的结果的反。
CMOS实现
- pMOS上拉网络:由三个并联的pMOS晶体管组成。只要有一个输入为低电平,pMOS晶体管导通,输出被拉高。
- nMOS下拉网络:由三个串联的nMOS晶体管组成。只有当所有输入都为高电平时,nMOS导通,输出被拉低。
因此,NOR3门输出为高电平的唯一情况是所有输入均为低电平,否则输出为低电平。
AND2 Gate (两输入AND门)
两输入AND门 是一个简单的逻辑门,其输出仅在两个输入都为高电平时为高,其余情况输出为低电平。
CMOS实现
- pMOS上拉网络:由两个并联的pMOS晶体管组成。当任意一个输入为低电平时,pMOS导通,输出被拉高。
- nMOS下拉网络:由两个串联的nMOS晶体管组成。当两个输入均为高电平时,nMOS导通,输出被拉低。
Transmission Gates (传输门)
传输门是CMOS电路中的一种开关电路,常用于连接和断开信号线。它克服了单独使用nMOS或pMOS时无法很好传输0或1的局限性。
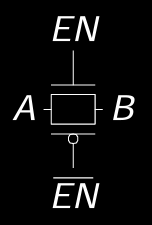
工作原理
- nMOS晶体管:擅长传输逻辑低电平(0),但传输高电平(1)性能较差。
- pMOS晶体管:擅长传输逻辑高电平(1),但传输低电平(0)性能较差。
通过将nMOS和pMOS晶体管并联,传输门能够高效传输逻辑0和逻辑1。其导通状态由控制信号 EN 决定:
- EN = 1:传输门开启,信号A与B相连,信号可以通过。
- EN = 0:传输门关闭,A与B断开,信号不通过。
传输门的优势在于能够同时很好地传递0和1,因此在多路复用器、锁存器等电路中有广泛应用。
Gordon Moore, 1929-
戈登·摩尔(Gordon Moore)是Intel公司的联合创始人之一,与罗伯特·诺伊斯(Robert Noyce)共同在1968年创立了这家半导体巨头。摩尔最著名的贡献之一就是提出了摩尔定律(Moore’s Law),即芯片上晶体管的数量大约每年翻一番。1965年,摩尔首次观察到这一趋势,后来又修订为晶体管数量每两年翻一番。这一规律在半导体产业中指导了数十年的技术进步,并引发了晶体管技术的快速发展。
- 摩尔定律的推论:
- 晶体管不仅越来越多,而且变得更快,功耗更低。
- 摩尔定律揭示了集成电路技术的指数增长,为现代计算技术的发展奠定了基础。
在图中可以看到从1970年代的Intel 4004处理器到2000年代的Core 2 Duo处理器,晶体管数量呈指数增长。摩尔定律形象地展示了集成电路技术的高速发展。
Power Consumption
功耗
功耗指的是一个设备在单位时间内消耗的能量,计算公式为: \[ \text{Power} = \frac{\text{Energy consumed}}{\text{Time}} \] 在数字设计中,功耗可以分为两种类型:
- Dynamic Power Consumption(动态功耗):主要与电路中信号的切换和电容的充放电有关。当晶体管的状态不断变化时,电路会消耗大量的动态功率。动态功耗的主要因素包括:
- 切换频率(信号翻转的速度)
- 电源电压(V\(_{DD}\))
- 电路中的负载电容
- Static Power Consumption(静态功耗):即电路在不切换状态时的功耗。静态功耗与泄漏电流密切相关,主要来源于晶体管在”关”状态下的漏电流。随着晶体管的缩小,漏电流变得越来越显著,因此即使电路没有切换,静态功耗也会不断增加。
管理和优化功耗是现代芯片设计中极为重要的一个方面,尤其是对于移动设备和嵌入式系统,低功耗设计往往是确保设备性能和续航的关键。
Dynamic Power Consumption(动态功耗)
动态功耗主要来源于晶体管在每个时钟周期中切换状态时所需的能量。每当晶体管的门电容充电时,电路就会消耗功率。其基本原理如下:
- 晶体管门电容的充电功耗:每次充电需要的能量是 \( CV_{DD}^2 \),其中 C 是电容,\( V_{DD} \) 是电源电压。
- 电路以频率 \( f \) 工作(每秒的周期数)。
- 电容在每个周期中被充电的次数是 \( \alpha \),称为活动因子(activity factor),表示电容在每个周期内的切换次数(从1到0的放电是免费的)。
动态功耗的计算公式为: \[ P_{\text{dynamic}} = \alpha C V_{DD}^2 f \] 公式中的各个参数可以直接影响电路的功耗。降低 \( V_{DD} \) 或减小频率 \( f \) 都可以减少动态功耗,因此低功耗设计中常通过降低电压和频率来实现能量的优化。
Activity Factor \( \alpha \) (活动因子)
活动因子 \( \alpha \) 代表电容在每个周期内充电的频率。不同的电路和数据模式下,活动因子会有所不同:
- 时钟信号:\( \alpha = 1 \),因为时钟在每个周期都切换。
- 数据每个周期切换一次:\( \alpha = 0.5 \)。
- 随机数据:\( \alpha = 0.25 \)。
- 典型数据:\( \alpha = 0.1 \)。
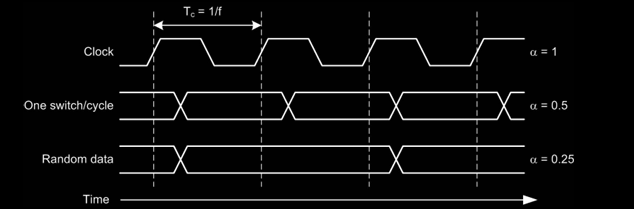
在实际应用中,典型数据模式下的活动因子通常较低,导致动态功耗的减少。
Static Power Consumption(静态功耗)
静态功耗是指当电路中的门不切换时所消耗的功耗,主要由泄漏电流引起。泄漏电流通常来自于晶体管即使在关闭时仍然存在的小电流。这一现象随着晶体管尺寸的缩小变得更加显著。
静态功耗的计算公式为: \[ P_{\text{static}} = I_{DD} V_{DD} \] 其中,\( I_{DD} \) 是静态电流(也称为漏电流),\( V_{DD} \) 是电源电压。减少静态功耗可以通过优化晶体管结构或使用较低的供电电压来实现。
Power Consumption Example(功耗实例)
在本节中,通过两个示例来估算手机运行应用程序或待机时的功耗。
运行 Angry Birds 时的功耗估算
我们假设手机运行 “Angry Birds” 应用时的参数如下:
- \( V_{DD} = 0.8 \,V \)(电源电压)
- \( C = 5 \,nF \)(电容)
- \( f = 2 \,GHz \)(时钟频率)
- \( \alpha = 0.1 \)(活动因子)
- \( I_{DD} = 100 \,mA \)(静态电流)
根据公式: \[ P_{\text{dynamic}} = \alpha C V_{DD}^2 f + I_{DD} V_{DD} \] 我们可以计算动态功耗: \[ P_{\text{dynamic}} = (0.1)(5 \,nF)(0.8 \,V)^2(2 \,GHz) + (100 \,mA)(0.8 \,V) \] 动态部分的功耗为: \[ = (0.64 + 0.08) \,W \approx 0.72 \,W \] 因此,运行该应用时的功耗约为 0.72瓦。
待机状态下的功耗估算
如果手机有一个 8瓦时的电池,并且在待机状态下,手机的功耗参数如下:
- \( V_{DD} = 0.8 \,V \)
- \( I_{DD} = 100 \,mA \)
静态功耗可以通过公式: \[ P_{\text{static}} = I_{DD} V_{DD} \] 进行计算: \[ P_{\text{static}} = (100 \,mA)(0.8 \,V) = 0.08 \,W \]
然后,电池的续航时间可以通过以下公式计算: \[ \text{Battery life} = \frac{\text{Capacity}}{\text{Consumption}} = \frac{8 \,W-hr}{0.08 \,W} = 100 \,hr = 4 \,days \] 因此,手机在待机状态下可以使用约 100小时,即 4天。