Chapter 2: Combinational Logic Design
《Digital Design and Computer Architecture: RISC-V Edition》
在数字设计与计算机体系结构的学习中,组合逻辑设计是关键的基础知识之一。组合逻辑电路(Combinational Circuits)是没有存储元素的逻辑电路,其输出仅由当前输入决定,不依赖于过去的输入或状态。这一章将带领我们深入了解组合逻辑电路的构成、布尔代数与方程、逻辑门、卡诺图等基本概念,以及与组合逻辑相关的时间和功能规范。
Chapter 2 :: Topics
这一章涵盖了以下几个主要主题:
- 组合电路(Combinational Circuits):分析没有反馈或记忆的电路,输入直接决定输出。
- 布尔方程(Boolean Equations):探讨如何通过布尔代数的运算来表达逻辑电路。
- 布尔代数(Boolean Algebra):深入研究使用布尔运算来简化和分析逻辑电路的技术。
- 从逻辑到门(From Logic to Gates):理解如何将逻辑表达式转换为实际的逻辑门实现。
- X 和 Z 的概念(X’s and Z’s, Oh My):讨论未定义的值(X)和高阻态(Z)在数字电路中的影响。
- 卡诺图(Karnaugh Maps):利用卡诺图简化逻辑表达式,降低电路复杂度。
- 组合电路构建模块(Combinational Building Blocks):介绍常用的组合电路模块如加法器、解码器和多路复用器。
- 时序分析(Timing):讨论电路中的延迟、建立时间、保持时间等时序问题。
通过这些主题的深入讲解,学生将掌握设计组合逻辑电路的基本技能,并理解它们如何在更大的计算机架构中起作用。
Combinational Circuits
组合电路是一种重要的逻辑电路,广泛应用于数字系统中。其输出仅取决于当前的输入,而不会存储任何过去的状态。与时序电路不同,组合电路没有记忆单元,因此是无状态的。
组合电路的组成
一个典型的逻辑电路由以下几个部分组成:
- 输入(Inputs):这些是电路接收到的外部信号,用来影响电路的行为。输入可以是二进制信号,表示为 0 或 1。
- 输出(Outputs):这是电路对给定输入的响应。组合电路的输出仅由当前输入决定,没有反馈路径。
- 功能规范(Functional Specification):描述电路应该执行的逻辑功能。例如,一个加法器电路的功能规范可能是将两个二进制数相加。
- 时序规范(Timing Specification):定义了电路中信号传播的时间要求。例如,信号从输入到输出所需的时间。

在这个组合逻辑电路的概念框架中,输入信号通过功能和时序规范的约束,最终生成对应的输出。简单的框图如上所示,其中输入经过功能和时序的定义,最终产生输出。
Circuits
电路是由多个逻辑元件组成的系统,每个元件根据输入信号执行特定的逻辑操作并生成输出信号。理解电路的结构和组成是学习组合逻辑设计的重要基础。
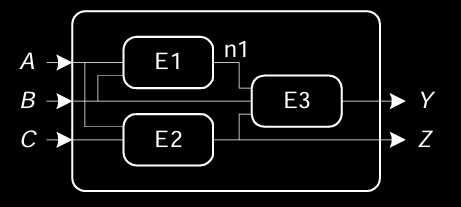
节点(Nodes)
电路中的节点指的是电路内部的连接点,它们包括输入节点、输出节点和内部节点:
- 输入节点:输入信号来自外部系统,用来驱动电路中的逻辑元件。在图示中,输入节点为 A、B、C。
- 输出节点:输出信号是电路根据输入信号处理后的结果。在图示中,输出为 Y 和 Z。
- 内部节点(n1):这是电路内部的连接点,可能连接多个逻辑元件,在逻辑处理的中间阶段起作用。
电路元件(Circuit Elements)
电路由多个逻辑元件组成,每个元件执行特定的逻辑功能。在图示中,E1、E2 和 E3 分别代表三个逻辑元件,它们共同处理输入 A、B、C,生成输出 Y 和 Z。每一个元件本身也是一个完整的电路,可以由其他逻辑门或子电路组成。
Types of Logic Circuits
逻辑电路的类型可以分为组合逻辑电路和时序逻辑电路。
组合逻辑(Combinational Logic)
组合逻辑电路的特点是无记忆性,输出仅由当前的输入值决定。输入信号在经过逻辑运算后立即生成相应的输出,没有反馈或状态保存。这类电路广泛应用于诸如加法器、编码器、解码器等数字系统中。
时序逻辑(Sequential Logic)
与组合逻辑不同,时序逻辑电路具有记忆性,其输出不仅依赖于当前的输入,还与之前的输入状态有关。这意味着时序逻辑电路在处理输入时会保存一些历史信息,常用于触发器和寄存器等电路中。时序逻辑电路不仅需要考虑功能规范,还必须处理时序规范,包括信号传播延迟等。
Rules of Combinational Composition
在设计组合电路时,需要遵循一些基本的规则,以确保电路的正确性和可操作性:
- 每个元件都是组合逻辑电路:电路中的每个元素都必须是组合逻辑电路,也就是说它们没有记忆单元,输出完全由输入决定。
- 每个节点要么是输入,要么连接到唯一一个输出:电路中的每个节点都必须清晰地定义为输入或输出的一部分,不能有模糊的连接或多重输出。
- 电路中不能包含循环路径(cyclic paths):组合逻辑电路必须是无反馈的,这意味着信号不能在电路中形成闭环,避免由于信号反复传播而导致的逻辑错误。
Example
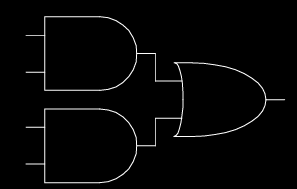
图示中的示例显示了由逻辑门组成的一个简单组合逻辑电路。这个电路没有任何循环路径,符合组合逻辑电路的构成规则。输入信号经过与非门和或门的处理,生成唯一的输出。
Boolean Equations
布尔方程
布尔方程是组合逻辑设计中的核心工具,它用数学表达式描述了输出如何根据输入的不同组合变化。在组合逻辑电路中,输出完全由输入的当前状态决定,布尔方程提供了清晰的功能规范,说明每个输入如何影响输出。
Example
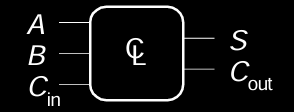
以一个简单的三输入电路为例,输入为 A、B 和 Cin,对应的输出为 S 和 Cout。布尔方程描述了 S 和 Cout 的功能关系:
-
\( S = A \oplus B \oplus C_{in} \)
这里的 S 是一个加法器电路的和输出,采用异或运算符(\(\oplus\))来计算。 -
\( C_{out} = AB + AC_{in} + BC_{in} \)
这个方程描述了进位输出 Cout,其中包括了输入的不同组合如何产生进位输出。
从逻辑电路图中可以看到,S 和 Cout 的功能分别由输入 A、B 和 Cin 决定,表示了一个典型的全加器电路模型。
Some Definitions
为了理解布尔方程,我们需要掌握一些重要的术语和概念:
- 补数(Complement):一个变量的补数是该变量取反的形式,通常在变量上方加一个横线表示,例如 \(\overline{A}\)、\(\overline{B}\)、\(\overline{C}\)。
- 文字(Literal):变量或其补数,例如 A、\(\overline{A}\)、B、\(\overline{B}\)、C、\(\overline{C}\)。
- 蕴含项(Implicant):由多个文字的乘积构成,例如 \(ABC\)、\(A\overline{C}\)、\(BC\)。
- 最小项(Minterm):包括所有输入变量的乘积。例如 \(ABC\)、\(A\overline{B}C\) 等等。
- 最大项(Maxterm):包含所有输入变量的和。例如 \((A + \overline{B} + C)\)、\((\overline{A} + B + C)\) 等。
这些定义帮助我们更好地理解如何使用布尔代数描述和简化逻辑表达式。
Sum-of-Products (SOP) Form
布尔方程可以采用积之和(SOP, Sum-of-Products)的形式来表达。积之和(Sum-of-Products, SOP)形式是布尔表达式的一种标准化方法,用于描述逻辑电路的输出。SOP 表示的是多个最小项(minterms)通过 OR 运算组合而成的表达式。每个最小项是通过 AND 运算将不同的输入组合在一起,当且仅当特定输入组合为真时,对应的最小项为真。
在这种形式下:
- 所有的布尔方程都可以转换为 SOP 形式。
- 每一行代表一个最小项(minterm)。
- 最小项是文字的乘积(AND),并且对于那一行(对应特定的输入组合)为真。
- 如果输出为 1,可以通过对这些最小项进行 OR 运算(加法)来生成整个函数。
例如,对于输入 A 和 B,输出 Y 可以如下表所示:
| A | B | Y | Minterm | Minterm Name |
|---|---|---|---|---|
| 0 | 0 | 0 | \(\overline{A} \overline{B}\) | \(m_0\) |
| 0 | 1 | 1 | \(\overline{A} B\) | \(m_1\) |
| 1 | 0 | 1 | \(A \overline{B}\) | \(m_2\) |
| 1 | 1 | 1 | \(A B\) | \(m_3\) |
对于每一行,最小项为真时,输出 Y 就为 1。整个 Y 的布尔方程可以写成:
\[ Y = m_1 + m_2 + m_3 = \overline{A}B + A\overline{B} + AB \]
这种 SOP 形式简洁且便于计算机和电路设计中实现组合逻辑电路。
Product-of-Sums (POS) Form
和之积(Product-of-Sums, POS)形式是另一种标准化布尔表达式的方式。与 SOP 相对,POS 是通过 AND 运算组合多个最大项(maxterms)而形成的表达式。每个最大项是通过 OR 运算组合不同输入的补数,当且仅当特定输入组合为假时,对应的最大项为真。
- 所有布尔方程也可以转化为 POS 形式。
- 每一行代表一个最大项。
- 每个最大项是文字的和(OR 运算)。
- 如果输出为 0,表示该行的最大项为真。
- 整个函数由 AND 运算将所有为真的最大项组合起来。
例子
对于相同的输入 A 和 B,输出 Y 表示如下:
| A | B | Y | Maxterm | Maxterm Name |
|---|---|---|---|---|
| 0 | 0 | 0 | \(A + B\) | \(M_0\) |
| 0 | 1 | 1 | \(A + \overline{B}\) | \(M_1\) |
| 1 | 0 | 0 | \(\overline{A} + B\) | \(M_2\) |
| 1 | 1 | 1 | \(\overline{A} + \overline{B}\) | \(M_3\) |
该函数 \(Y = F(A, B)\) 的 POS 表示为:
\[ Y = (A + B)(\overline{A} + B) \]
在这种形式下,将所有为假的行组合为和,通过 AND 运算得到整个逻辑表达式。
Boolean Equations Example 布尔方程示例
布尔方程可以帮助解决日常逻辑问题。比如一个例子:
- 你要去自助餐厅吃午饭,但如果下面两种情况之一发生,你不会吃饭(E = 0):
- 餐厅不干净(C = 0)。
- 餐厅只供应肉饼(M = 1)。
根据这些条件,我们可以构建一个布尔真值表,描述你是否会吃午饭(E):
| C | M | E |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
根据这个表格,C 和 M 的组合可以通过布尔方程表示,来判断你是否会选择吃午饭。
SOP & POS Form
SOP – Sum-of-Products 形式
在 SOP 形式 中,逻辑表达式是由多个最小项(minterms)的乘积(AND 运算)通过加法(OR 运算)组合而成的。对于某些输入组合,当输出为 1 时,我们会通过 OR 运算将对应的最小项连接起来。例如,在下表中,C 和 M 是输入,E 是输出:
| C | M | E | 最小项 |
|---|---|---|---|
| 0 | 0 | 0 | \(\overline{C} \overline{M}\) |
| 0 | 1 | 0 | \(\overline{C} M\) |
| 1 | 0 | 1 | \(C \overline{M}\) |
| 1 | 1 | 0 | \(C M\) |
输出 E 的表达式为: \[ E = \overline{C} M \] 简化为: \[ E = \Sigma(2) \] 其中,Σ 表示最小项的和,索引 2 代表输出为 1 的行。
POS – Product-of-Sums 形式
在 POS 形式 中,逻辑表达式由多个最大项(maxterms)的和(OR 运算)通过乘积(AND 运算)组合而成。当某些输入组合输出为 0 时,我们会用 AND 运算连接这些最大项。在下表中,C 和 M 是输入,E 是输出:
| C | M | E | 最大项 |
|---|---|---|---|
| 0 | 0 | 0 | \(C + M\) |
| 0 | 1 | 0 | \(C + \overline{M}\) |
| 1 | 0 | 1 | \(\overline{C} + M\) |
| 1 | 1 | 0 | \(\overline{C} + \overline{M}\) |
输出 E 的表达式为: \[ E = (C + M)(C + \overline{M})(\overline{C} + \overline{M}) \] 简化为: \[ E = \Pi(0, 1, 3) \] 其中,Π 表示最大项的积,索引 0、1 和 3 代表输出为 0 的行。
Forming Boolean Expressions 形成布尔表达式
Example 1
问题描述:如果不下雨(\(\overline{R}\))并且有三明治(S),我们就去公园(P 为输出)。
布尔表达式: \[ P = \overline{R} S \] 这里,\(\overline{R}\) 表示“没有下雨”,S 表示“有三明治”。
Example 2
问题描述:如果我们给你寄了一百万美元(M)或一个小笔记本(N),你将被视为赢家(W 为输出)。
布尔表达式: \[ W = M + N \] 这个表达式表示,只要满足任意一个条件,你就会被视为赢家。
Example 3
问题描述:如果你自己做饭(M)或者你有一个非常有才华但不昂贵的私人厨师(C, T, \(\overline{X}\)),你可以吃到美味的食物(E 为输出)。
布尔表达式: \[ E = M + (C T \overline{X}) \] 这里,\(M\) 表示“你自己做饭”,\(C T \overline{X}\) 表示“有才华(T)但不昂贵(\(\overline{X}\))的厨师(C)”。
通过这些例子,我们可以看到如何将日常逻辑问题转换为布尔表达式,以便在逻辑电路中使用。
Boolean Axioms
布尔公理
布尔代数中的公理提供了简化和操作布尔表达式的基本规则。这些公理与二进制运算密切相关,能够帮助我们理解逻辑表达式的本质并进行简化。
常见的布尔代数公理
-
A1: \( B = 0 \) 当 \( B \neq 1 \)(二进制场 Binary Field)
这是二进制系统的基础,变量 B 的值只能是 0 或 1。 -
A2: \(\overline{0} = 1\)(NOT 运算)
任何输入为 0 的取反结果是 1,这是逻辑运算中的非(NOT)操作的基础。 -
A3: \( 0 \cdot 0 = 0 \)(AND/OR 运算)
当两个输入都为 0 时,其 AND 运算结果为 0。 -
A4: \( 1 \cdot 1 = 1 \)(AND/OR 运算)
当两个输入都为 1 时,其 AND 运算结果为 1。 -
A5: \( 0 \cdot 1 = 1 \cdot 0 = 0 \)
当一个输入为 0 另一个为 1 或者两者都为 0 时,AND 运算结果为 0。
公理的双重性(Duality)
布尔代数中的双重性原则允许我们通过将 AND 替换为 OR,将 0 替换为 1,来得出对偶规则。每个公理都有对应的对偶规则:
- A1 对偶: \( B = 1 \) 当 \( B \neq 0 \)
- A2 对偶: \(\overline{1} = 0\)
- A3 对偶: \( 1 + 1 = 1 \)
- A4 对偶: \( 0 + 0 = 0 \)
- A5 对偶: \( 1 + 0 = 0 + 1 = 1 \)
这些对偶规则展示了逻辑运算中的对称性,帮助简化表达式时快速识别出相应的替换规则。
Boolean Theorems of One Variable
单变量布尔定理
布尔代数中的单变量定理为简化逻辑表达式提供了基本工具。通过这些定理,我们可以将复杂的布尔表达式简化为更易于实现和理解的形式。每个定理都展示了布尔代数的独特特性,以及如何通过逻辑运算简化变量之间的关系。
常见定理
-
T1: \( B \cdot 1 = B \)(恒等定理 Identity)
一个布尔变量与 1 进行 AND 运算的结果是变量本身。 -
T2: \( B \cdot 0 = 0 \)(空元素定理 Null Element)
任何布尔变量与 0 进行 AND 运算的结果都是 0。 -
T3: \( B + B = B \)(幂等定理 Idempotency)
一个布尔变量与自身进行 OR 运算的结果是该变量本身。 -
T4: \(\overline{\overline{B}} = B\)(二次补运算 Involution)
一个布尔变量的两次取反结果是该变量本身。 -
T5: \( B \cdot \overline{B} = 0 \)(互补定理 Complements)
一个布尔变量与其补数进行 AND 运算的结果是 0。
对偶原则
这些定理也可以通过对偶原则生成新的规则。使用对偶操作符替换 AND 为 OR,0 为 1,就可以生成对应的对偶定理,进一步丰富简化布尔表达式的工具集。
T1: Identity Theorem(恒等定理)
- \( B \cdot 1 = B \)
- \( B + 0 = B \)
这个定理表明,任何布尔变量与 1 进行 AND 运算的结果是变量本身,与 0 进行 OR 运算的结果也是变量本身。该定理对应了布尔代数中的恒等操作。
T2: Null Element Theorem(零元定理)
- \( B \cdot 0 = 0 \)
- \( B + 1 = 1 \)
该定理描述了当布尔变量与 0 进行 AND 运算时,结果总是 0;当与 1 进行 OR 运算时,结果总是 1。零元定理说明了 0 和 1 在布尔代数中的特殊角色。
T3: Idempotency Theorem(幂等定理)
- \( B \cdot B = B \)
- \( B + B = B \)
幂等定理表明,布尔变量与自身进行 AND 或 OR 运算时,结果总是变量本身。这强调了布尔变量的自保持特性,无论运算几次结果都不变。
T4: Involution Theorem(二次补运算定理)
- \( \overline{\overline{B}} = B \)
该定理揭示了取反运算的特性:任何布尔变量的两次取反将恢复为变量本身。这个定理在逻辑电路中表示,一个信号的两次取反会返回其原始状态。
T5: Complement Theorem(互补定理)
- \( B \cdot \overline{B} = 0 \)
- \( B + \overline{B} = 1 \)
互补定理展示了布尔变量与其补数的关系:一个变量与其补数进行 AND 运算时,结果总是 0;进行 OR 运算时,结果总是 1。这是布尔代数中非常重要的特性,说明了互补关系在逻辑运算中的不可避免性。
Recap: Basic Boolean Theorems
我们回顾了基本的布尔代数定理,这些定理为简化逻辑表达式提供了重要的基础。每个定理都有对应的对偶形式,展示了布尔代数中的双重性原则。
基本布尔定理
- T1: Identity Theorem \( B \cdot 1 = B \)
对偶:\( B + 0 = B \) - T2: Null Element Theorem \( B \cdot 0 = 0 \)
对偶:\( B + 1 = 1 \) - T3: Idempotency Theorem \( B \cdot B = B \)
对偶:\( B + B = B \) - T4: Involution Theorem \( \overline{\overline{B}} = B \)
- T5: Complement Theorem \( B \cdot \overline{B} = 0 \)
对偶:\( B + \overline{B} = 1 \)
Boolean Algebra: Theorems of Several Variables
布尔代数:多变量定理
在布尔代数中,除了单变量定理之外,多变量定理提供了更多的工具用于复杂逻辑表达式的简化。以下是几条重要的多变量定理。
多变量布尔定理及其对偶
-
T6: Commutativity (交换律)
\( B \cdot C = C \cdot B \)
对偶:\( B + C = C + B \) -
T7: Associativity (结合律)
\( (B \cdot C) \cdot D = B \cdot (C \cdot D) \)
对偶:\( (B + C) + D = B + (C + D) \) -
T8: Distributivity (分配律)
\( B \cdot (C + D) = (B \cdot C) + (B \cdot D) \)
对偶:\( B + (C \cdot D) = (B + C) \cdot (B + D) \)
注意:T8’ 不同于传统代数,OR(+)可以在 AND(·)上分配。 -
T9: Covering (覆盖定理)
\( B \cdot (B + C) = B \)
对偶:\( B + (B \cdot C) = B \) -
T10: Combining (合并定理)
\( B \cdot C + B \cdot \overline{C} = B \)
对偶:\( (B + C) \cdot (B + \overline{C}) = B \) -
T11: Consensus (一致性定理)
\( (B \cdot C) + (B \cdot D) + (C \cdot D) = (B \cdot C) + (B \cdot D) \)
对偶:\( (B + C) \cdot (B + D) \cdot (C + D) = (B + C) \cdot (B + D) \)
这些定理用于处理多个变量的逻辑表达式,帮助我们有效简化复杂的逻辑系统。
How to Prove
证明布尔代数中的定理或简化逻辑表达式有两种主要方法:
-
方法 1:完美归纳法(Perfect Induction)
通过列举所有可能的输入组合,验证表达式的真值表是否一致。 -
方法 2:利用其他定理和公理简化方程
使用已知的布尔代数定理和公理来一步步简化表达式,使其左侧和右侧相等。例如,可以将一边的表达式转换为另一边的形式。
这两种方法在实际中都被广泛使用,特别是在验证复杂的逻辑电路时。
T10: Combining Theorem
定理 T10: \( (B \cdot C) + (B \cdot \overline{C}) = B \)
该定理称为“合并定理”(Combining Theorem),说明了一个变量与其两个互补部分的 AND 运算结果可以通过 OR 运算组合简化为该变量本身。
证明方法
利用布尔代数的分配律和互补定理,可以证明该定理。具体步骤如下:
-
分配 \( B \): \[ (B \cdot C) + (B \cdot \overline{C}) = B \cdot (C + \overline{C}) \]
-
根据互补定理 \( C + \overline{C} = 1 \),简化: \[ B \cdot 1 = B \]
因此,证明了 \( (B \cdot C) + (B \cdot \overline{C}) = B \)。
De Morgan’s Theorem: Dual
定理 T12: De Morgan 定理
De Morgan 定理描述了布尔表达式中取反运算的分配规则。该定理有两种形式:
-
形式 1: \[ \overline{B \cdot C \cdot D} = \overline{B} + \overline{C} + \overline{D} \]
即,乘积的补数等于补数的和。 -
形式 2: \[ \overline{B + C + D} = \overline{B} \cdot \overline{C} \cdot \overline{D} \]
即,和的补数等于补数的乘积。
De Morgan 定理在逻辑电路设计中非常重要,尤其是在逻辑表达式的简化和电路实现中。
总结
- 乘积的补数是补数的和。
- 和的补数是补数的乘积。
Recap: Theorems of Several Variables
让我们回顾多变量布尔定理及其对应的对偶形式。每个定理都展示了在处理多个变量时如何简化复杂的布尔表达式。
多变量定理及其对偶
-
T6: 交换律 (Commutativity)
\( B \cdot C = C \cdot B \)
对偶:\( B + C = C + B \) -
T7: 结合律 (Associativity)
\( (B \cdot C) \cdot D = B \cdot (C \cdot D) \)
对偶:\( (B + C) + D = B + (C + D) \) -
T8: 分配律 (Distributivity)
\( B \cdot (C + D) = (B \cdot C) + (B \cdot D) \)
对偶:\( B + (C \cdot D) = (B + C) \cdot (B + D) \) -
T9: 覆盖定理 (Covering)
\( B \cdot (B + C) = B \)
对偶:\( B + (B \cdot C) = B \) -
T10: 合并定理 (Combining)
\( (B \cdot C) + (B \cdot \overline{C}) = B \)
对偶:\( (B + C) \cdot (B + \overline{C}) = B \) -
T11: 一致性定理 (Consensus)
\( (B \cdot C) + (B \cdot D) + (C \cdot D) = (B \cdot C) + (B \cdot D) \)
对偶:\( (B + C) \cdot (B + D) \cdot (C + D) = (B + C) \cdot (B + D) \) -
T12: De Morgan 定理
\( \overline{B \cdot C \cdot D} = \overline{B} + \overline{C} + \overline{D} \)
对偶:\( \overline{B + C + D} = \overline{B} \cdot \overline{C} \cdot \overline{D} \)
这些定理在逻辑电路设计中应用广泛,帮助工程师优化电路并减少逻辑门的数量。
Boolean Algebra: Simplifying Equations
布尔代数:简化方程
简化布尔表达式是逻辑设计的核心任务之一,目的是减少表达式的复杂性,从而降低实现逻辑电路所需的逻辑门数量、功耗和成本。简化的结果通常采用 乘积之和(SOP)形式,这种形式包含最少的蕴含项(implicants),且每个蕴含项中的文字(literals)数量最少。
关键术语
- 蕴含项(Implicant):由多个文字的乘积构成,如 \( ABC \)、\( A\overline{C} \)、\( B\overline{C} \)。
- 文字(Literal):变量本身或其补数,如 \( A \)、\( \overline{A} \)、\( B \)、\( C \)、\( \overline{C} \)。
除了减少文字和蕴含项的数量,简化还可以意味着减少电路所需的门数量、降低功耗、降低延迟等。例如,异或操作 \( Y = A \oplus B \) 可能比最小的乘积之和形式 \( Y = AB + \overline{A}\overline{B} \) 更容易实现,这取决于具体的技术和设计需求。
Simplifying Boolean Equations
Example
简化表达式:
\[ Y = \overline{A}B + AB \]
通过 T10: Combining Theorem(合并定理),该表达式可以直接简化为: \[ Y = B \]
或者,使用分配律简化:
- \( Y = B(A + \overline{A}) \) (T8: Distributivity 分配律)
- \( A + \overline{A} = 1 \) (T5’: Complements 互补定理)
- \( Y = B \cdot 1 = B \) (T1: Identity 恒等定理)
Example
简化表达式:
\[ Y = A\overline{B}C + ABC + \overline{A}BC \]
-
应用幂等定理 \(ABC +ABC = ABC \): \[ Y = A\overline{B}C + ABC + ABC + \overline{A}BC \] (T3’: Idempotency 幂等定理)
-
使用结合律将项进行分组: \[ Y = (\overline{A}BC + ABC) + (ABC + A\overline{B}V) \] (T7’: Associativity 结合律)
-
使用合并定理简化各组: \[ \overline{A}BC + ABC = BC \]
\[ ABC + A\overline{B}C = AC \]
最终结果为: \[ Y = BC + AC \] (T10: Combining 合并定理)
lifying Boolean Equations
Example
简化表达式:
\[ Y = A(AB + ABC) \]
使用布尔代数定理对表达式进行简化:
-
使用幂等定理(T3’),我们知道 \( AB + ABC = AB \): \[ Y = A \cdot AB \]
-
再使用幂等定理: \[ A \cdot AB = AB \]
因此,简化后的表达式为: \[ Y = AB \]
Example
简化表达式:
\[ Y = \overline{A}BC + \overline{A} \]
首先,注意到重复的变量 \( \overline{A} \),我们可以应用覆盖定理(T9’):
- 使用覆盖定理 \( \overline{A} + \overline{A}BC = \overline{A} \): \[ Y = \overline{A} \]
最终简化结果为: \[ Y = \overline{A} \]
Multiplying Out: SOP Form
SOP(Sum-of-Products)形式是布尔表达式的一种标准化表示形式,其中每个乘积项仅包含文字(即变量或其补数)。在设计逻辑电路时,SOP 形式常被用来实现逻辑表达式,因为它们可以直接对应到逻辑门的实现。
Example
简化表达式:
\[ Y = (A + C + D + E)(A + B) \]
首先使用分配律(T8’):
-
分配 \( (A + B) \) 到每个项: \[ Y = A(A + B) + C(A + B) + D(A + B) + E(A + B) \]
-
使用幂等定理 \( A + A = A \) 和分配律 \( A \cdot A = A \): \[ Y = A + AC + AD + AE + BC + BD + BE \]
最终表达式为: \[ Y = A + BC + BD + BE \]
Literal and Implicant Ordering
- 变量顺序:在蕴含项中,变量应按字母顺序排列。
- 蕴含项顺序:蕴含项的顺序无关紧要,不影响表达式的等价性。
Review: Canonical SOP & POS Forms
SOP 形式(Sum-of-Products)
SOP 形式将布尔表达式转换为一组乘积项的和,每一项都是文字的乘积。以下是一个真值表对应的 SOP 形式:
-
SOP 形式: \[ E = CM \]
这是根据真值表得出的最简 SOP 形式。
POS 形式(Product-of-Sums)
POS 形式是将布尔表达式写为一组和项的积,每一项都是变量的和。以下是真值表对应的 POS 形式:
- POS 形式: \[ E = (C + M)(C + \overline{M})(\overline{C} + \overline{M}) \]
SOP 和 POS 形式表达的是相同的逻辑功能,只是在实现逻辑电路时需要根据不同的需求选择适合的形式。
Factoring: POS Form
POS 形式简介
POS (Product-of-Sums) 形式是布尔表达式的一种标准化形式,每一项都是和的形式,即每一项仅包含变量或其补数的和。POS 形式通常用于描述逻辑函数的最简和表达。
-
POS 形式:
\( Y = (A+B)(C+D)(E’+F) \) -
不是 POS 形式:
\( Y = (D+E)(F’+GH) \) -
POS 形式:
\( Z = A(B+C)(D+E’) \)
POS 形式确保表达式中的每个和项都仅包含文字(变量或补数),方便逻辑设计中的实现。
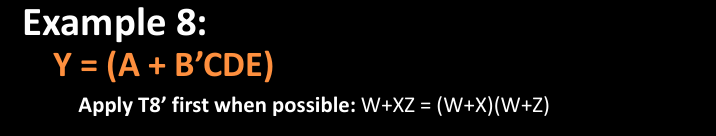

De Morgan’s Theorem
De Morgan 定理帮助我们将布尔表达式中的乘积转换为和,或将和转换为乘积,特别是在取反的情况下。


Common Errors in Boolean Algebra: Simplifying Equations
在简化布尔方程的过程中,常见的错误可能会导致错误的结果或增加理解和推导的难度。通过识别这些常见错误,可以帮助避免不必要的麻烦,提高逻辑表达式简化的准确性和效率。
Common Errors
-
使用撇号(
')而不是变量上方的横线表示取反:
当手写方程时,撇号容易丢失,使用横线更直观和明确。 -
未保持对齐:
在步骤之间未保持对齐,容易让人看不清变化的部分。保持对齐有助于查看哪些部分发生了变化,帮助解决问题和检查。 -
一次性对同一项应用多个定理:
每次只应用一个定理,避免过多步骤同时进行,增加错误风险。 -
应用自创的“个人定理”:
应该严格按照已知的布尔定理进行简化,而不是发明自己的规则。 -
几乎应用了正确的定理:
有时候看似正确的定理实际上并不适用。确保每次应用的定理准确无误。 -
未利用合并、覆盖和分配律(特别是对偶形式):
这些定理和简化方法是简化布尔方程的关键工具,应该充分利用。
Additional Common Errors
-
丢失横线(或撇号):
这一错误会导致取反的部分被忽略,从而影响表达式的正确性。保持对齐有助于避免此类错误。 -
丢失项:
在简化过程中,如果省略了一些变量或项,可能会导致错误的表达式。 -
尝试一次性完成多步操作:
一次完成太多步骤往往容易出错,应该分步进行。 -
错误应用定理:
-
错误: \( ABC + \overline{A}BC = B \)
正确: \( ABC + \overline{A}BC = AC \)
合并定理只允许合并在某一个变量上相差的项。 -
错误: \( A + \overline{A} = 0 \)
正确: \( A + \overline{A} = 1 \)
这是互补定理的基本规则。 -
错误: \( A \cdot \overline{A} = 1 \)
正确: \( A \cdot \overline{A} = 0 \) -
错误: \( ABC = B \)
正确: \( B + ABC = B \)
在覆盖定理中,必须有与其他项涵盖的相同项。 -
错误: \( \overline{AC} = \overline{A}·\overline{C} \)
正确: \( \overline{AC} = \overline{A} + \overline{C} \)
使用 De Morgan 定理正确转换取反。 -
错误: \( \overline{A + C} = \overline{A} + \overline{C} \)
正确: \( \overline{A + C} = \overline{A}·\overline{C} \)
使用 De Morgan 定理需要注意和积之间的转换。
-
Common Errors with De Morgan’s Theorem
使用 De Morgan 定理时,常见的错误主要涉及运算的顺序和取反规则的应用。
-
没有从外部的括号开始操作:
应从最外层的括号开始逐步工作,逐层处理,以确保简化过程的清晰性。 -
试图将 De Morgan 定理应用于整个复杂表达式:
De Morgan 定理只能应用于 AND 或 OR 运算符下的项,不能直接对整个表达式进行处理。 - 丢失横线:
应用 De Morgan 定理时,确保横线(或撇号)覆盖整个需要取反的部分。
步骤:- 将 AND 转换为 OR(或将 OR 转换为 AND)。
- 保留项。
- 将横线放在每个单独的项上。
- 没有保持项的关联性(丢失括号):
括号的丢失会破坏表达式的结构,例如:- 错误: \( (ABC)’C + D’ = A’B’C’ + C + D’ \)
- 正确: \( (ABC)’C + D’ = (A’ + B’ + C’)C + D’ = A’B’C’ + D’ \)
通过避免这些常见的错误,可以更准确地简化布尔表达式,提高逻辑设计的效率。
From Logic to Gates
在将逻辑表达式转换为逻辑门电路时,我们需要理解每个逻辑操作符对应的基本逻辑门,并按表达式的结构连接这些逻辑门。以下是将布尔表达式转换为电路的过程。
Example
构建以下逻辑表达式的电路:
\[ Y = A\overline{B} + \overline{C}DE \]
- 第一部分:\( A\overline{B} \)
- 使用一个 NOT 门 对 \( B \) 进行取反,得到 \( \overline{B} \)。
- 使用一个 AND 门 将 \( A \) 和 \( \overline{B} \) 连接,得到 \( A\overline{B} \)。
- 第二部分:\( \overline{C}DE \)
- 使用一个 NOT 门 对 \( C \) 进行取反,得到 \( \overline{C} \)。
- 使用一个 AND 门 将 \( \overline{C} \)、\( D \)、和 \( E \) 连接,得到 \( \overline{C}DE \)。
- 组合:
- 使用一个 OR 门 将两个 AND 门的输出 \( A\overline{B} \) 和 \( \overline{C}DE \) 相连,得到输出 \( Y \)。
Circuit Schematic Rules
在绘制逻辑电路图时,应遵循以下基本规则:
- 输入端在左侧(或顶部):逻辑电路的输入通常位于左侧或顶部。
- 输出端在右侧(或底部):电路的输出应位于右侧或底部。
- 逻辑门从左到右流动:电路中信号的流动方向应从左到右,保持逻辑顺序。
- 尽量使用直线连接:避免不必要的弯曲,保持电路简洁明了。
示例电路图中,\( A \) 和 \( B \) 通过一个 AND 门相连,\( C \)、\( D \)、\( E \) 也通过 AND 门相连,最后两个输出通过 OR 门结合生成输出 \( Y \)。
Circuit Schematic Rules (cont.)
进一步的电路图规则包括:
- T 形接头处的线相连:当三条导线在 T 形接头处相交时,表示它们相连。
- 导线交叉时有点表示连接:当两条导线相交时,如果交叉处有点,表示它们相连。
- 无点交叉的导线不相连:当导线交叉时,如果没有点,则表示它们不相连。
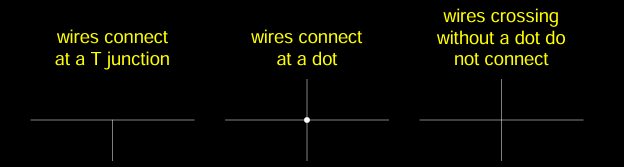
这些规则有助于确保电路图的可读性和逻辑正确性,避免理解上的误差。
Two-Level Logic
两级逻辑是指逻辑电路中常见的一种设计结构,它由两层逻辑门组成,通常是 AND 门 和 OR 门 的组合。该设计的特点是:
- 第一层使用 AND 门进行乘积运算。
- 第二层使用 OR 门对 AND 门的输出进行求和。
Example
\[ Y = \overline{A}\overline{B}C + A\overline{B}C + \overline{A}BC \]
该表达式包含三个 AND 项(\(\overline{A}\overline{B}C\)、\(A\overline{B}C\)、\(\overline{A}BC\)),然后通过 OR 门组合成最终输出 \( Y \)。这种形式的电路被称为两级逻辑,因为它由两层逻辑运算构成。
Multilevel Logic
相比于两级逻辑,多级逻辑更复杂,通常由多层简单的逻辑门构成。通过多个逻辑门级联,可以实现更复杂的逻辑功能。
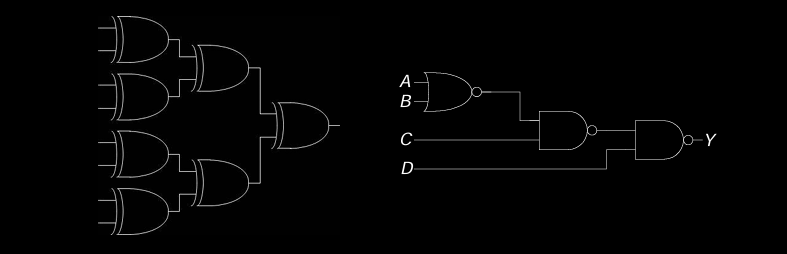
- 多级逻辑允许通过多层逻辑门来逐步处理输入信号,从而实现复杂的逻辑功能。
- 如图所示的电路中,多个 AND 门和 OR 门组合在一起,形成了一个多级逻辑电路。
优点
- 多级逻辑的设计更灵活,适用于实现复杂的逻辑关系。
缺点
- 由于信号需要经过多层逻辑门,可能会增加延迟和功耗。
Multiple-Output Circuits
在某些情况下,一个电路可能有多个输出。例如,优先电路(Priority Circuit)是一个多输出电路的典型示例,它的输出基于输入的优先级顺序。
Example: Priority Circuit
- 当多个输入信号为 真(1) 时,电路输出中只会根据具有最高优先级的输入对应的输出为 真,其他输出为 假(0)。
- 在真值表中,输入 \( A_3 \)、\( A_2 \)、\( A_1 \)、\( A_0 \) 具有优先级,输出 \( Y_3 \)、\( Y_2 \)、\( Y_1 \)、\( Y_0 \) 依次表示最优先的输入信号。
硬件实现中,每个输出信号 \( Y_n \) 表示输入中具有最高优先级的那个信号。优先电路常用于需要根据优先级选择输入的场景,如中断请求处理器和调度器。
Don’t Cares in Logic Design
在逻辑设计中,”不关心”(Don’t Care)条件是指在某些输入组合下,输出无所谓是1还是0的情况。这些条件可以帮助我们在设计逻辑电路时进一步简化表达式,减少逻辑门的使用数量。
在优先电路的真值表中,有时某些输入组合不会出现在实际操作中,或对输出的影响无关紧要。在这种情况下,我们可以自由选择这些条件下的输出值,以便使用更少的逻辑门来实现功能。
例子
在图表中的真值表中,某些行对应的输出是 “不关心” 的情况。通过在设计时充分利用这些 “不关心” 的输入组合,可以简化逻辑表达式,减少硬件复杂度。
Two-Level Logic Forms
两级逻辑是最常见的组合逻辑形式,特别适合实现逻辑方程。两级逻辑的基本形式可以是 AND 后跟 OR(即 SOP 形式),或 OR 后跟 AND(即 POS 形式)。
Two-Level Logic Variations
- SOP 形式: AND 门先执行操作,结果由 OR 门组合。这是两级逻辑中最常见的形式。
- 例子:\( Y = A\overline{B}C + AB\overline{C} + A\overline{B}\overline{C} \)
- POS 形式: OR 门先操作,结果由 AND 门组合。这种形式对于某些逻辑电路设计可能更合适。
- 例子:\( Y = (A + \overline{B})(B + C)(A + \overline{C}) \)
-
仅使用 NAND 门: NAND 门逻辑是 AND 和 NOT 门的组合,可以用于实现 SOP 形式的逻辑。
- 仅使用 NOR 门: NOR 门逻辑是 OR 和 NOT 门的组合,适用于实现 POS 形式的逻辑。
Two-Level Logic Variation
在两级逻辑中,也可以有变体,例如 ORs 后跟 ANDs。对于这些情况,我们使用 POS 形式 来表示。
Example
\[ Y = (\overline{A} + \overline{B})(A + B + \overline{C}) \]
在这个例子中,OR 操作先执行,然后再通过 AND 门组合输出。
Two-Level Logic
在数字电路设计中,两级逻辑结构通常涉及两层逻辑门操作。最常见的两级逻辑是 SOP(Sum of Products) 和 POS(Product of Sums) 形式,这些形式有助于简化复杂的逻辑表达式并优化电路设计。
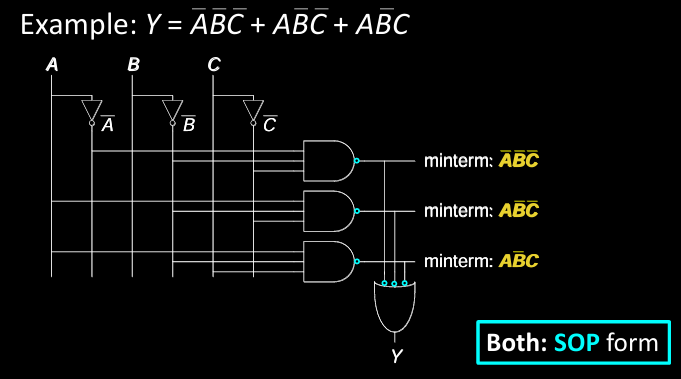
Example 1: ANDs followed by ORs (SOP Form)
- 形式: AND 门后接 OR 门(SOP 形式)。
- 示例:
\[ Y = \overline{A}\overline{B}C + A\overline{B}C + \overline{A}BC \]- 每个项通过 AND 门生成,其中一些输入经过取反(NOT 门)。
- 最后使用 OR 门将各个 AND 门的输出组合在一起,生成输出 \( Y \)。
- 这是一个 SOP(乘积和) 形式的两级逻辑,因为它从 AND 操作开始,最后通过 OR 门将结果求和。
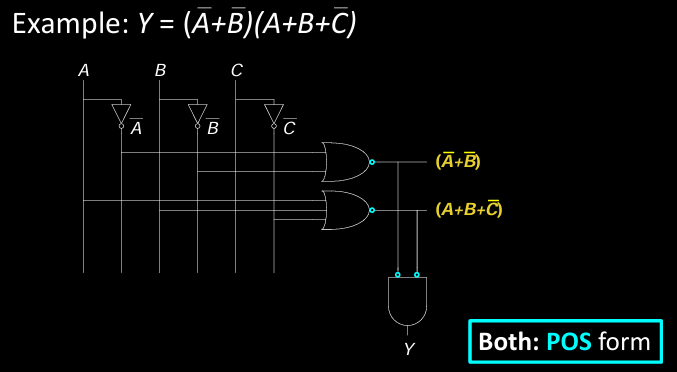
Example 2: ORs followed by ANDs (POS Form)
- 形式: OR 门后接 AND 门(POS 形式)。
- 示例:
\[ Y = (\overline{A} + \overline{B})(A + B + \overline{C}) \]- OR 门首先对输入进行逻辑求和。
- 然后使用 AND 门将两个 OR 门的输出组合在一起,生成最终输出 \( Y \)。
- 这是 POS(和的积) 形式的两级逻辑,因为它从 OR 操作开始,最后通过 AND 门求积。
两级逻辑常见形式
- ANDs followed by ORs: 对应 SOP 形式,是最常见的两级逻辑设计形式。
- ORs followed by ANDs: 对应 POS 形式,是两级逻辑的另一种变体。
- 仅使用 NAND 门: 可以实现 SOP 形式的电路。
- 仅使用 NOR 门: 可用于实现 POS 形式的电路。
Bubble Pushing
Bubble Pushing 是一种在逻辑设计中使用的技巧,特别是在转换 NAND 和 NOR 门时非常有用。通过在电路中适当推送或消除反相器(“泡泡”表示反相),可以将 NAND 和 NOR 门转换为等效的其他门形式,同时保持电路的功能不变。
这种技术依赖于 De Morgan 定理,它帮助我们在处理复杂逻辑表达式时简化和转换逻辑门。
De Morgan’s Theorem
De Morgan 定理为布尔代数中的乘积和和的转换提供了规则。通过 De Morgan 定理,可以将 AND 门和 OR 门在取反操作下相互转换。
- 定理:
\[ \overline{B \cdot C \cdot D} = \overline{B} + \overline{C} + \overline{D} \]- 将一个乘积(AND)取反等同于对每个项取反后进行和(OR)运算。
- 对偶:
\[ \overline{B + C + D} = \overline{B} \cdot \overline{C} \cdot \overline{D} \]- 将和(OR)取反等同于对每个项取反后进行乘积(AND)运算。


De Morgan’s Theorem Applied to Gates
De Morgan 定理不仅适用于逻辑表达式的简化,也能在电路设计中帮助转换逻辑门。
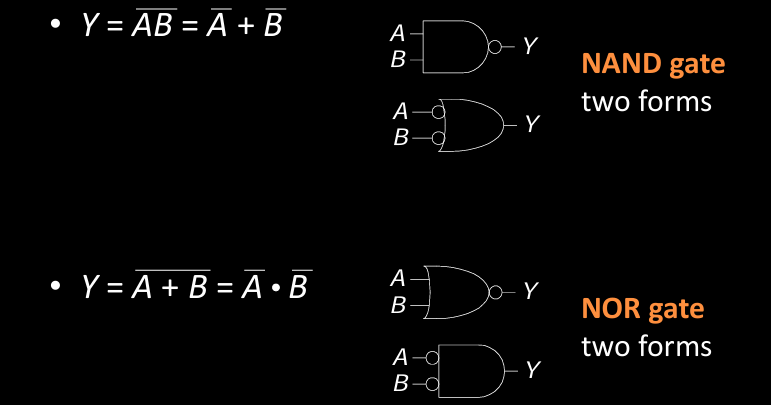
-
NAND 门形式:
对于 \( \overline{A \cdot B} = \overline{A} + \overline{B} \),可以使用两个 NOT 门和一个 OR 门来实现。 -
NOR 门形式:
对于 \( \overline{A + B} = \overline{A} \cdot \overline{B} \),可以使用两个 NOT 门和一个 AND 门来实现。
这些转换方式使得 NAND 和 NOR 门能够灵活地实现其他逻辑操作,并且在设计中能减少门的使用数量。
Bubble Pushing
反向操作(Backward Transformation)
在反向操作中,门体会发生变化,通常涉及对输入添加反向泡泡。通过这种方式,可以将 NAND 和 NOR 门转换为等效的逻辑形式。
- 例如:在下图中,NAND 门转换成了一个 OR 门,且其输入端都加上了泡泡(反向符号),确保逻辑功能不变:
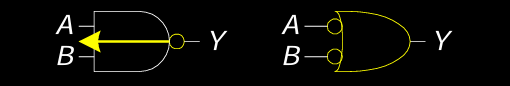
\[ A \cdot B \text{(NAND)} \rightarrow \overline{A} + \overline{B} \text{(OR)} \]
规则
- 从输出开始,逐步向输入推移:首先确定最终的输出形式,然后根据反向符号的需求逐步向输入推进。
- 在最终输出推送泡泡:推送泡泡直到达到输入,使得最终输出形式与逻辑要求一致。
- 绘制门时,使泡泡可以相互抵消:通过适当的门和连接设计,消除多余的泡泡,简化电路。
练习
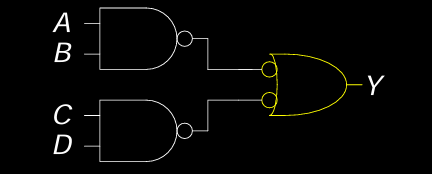
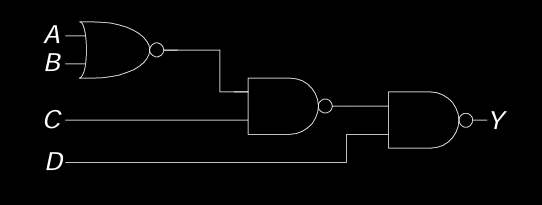
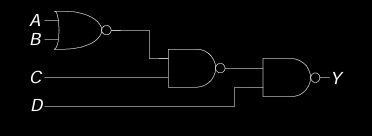
X’s and Z’s in Combinational Logic
组合逻辑中的 X 和 Z
在数字设计和组合逻辑中,X 和 Z 是表示特定状态的符号,主要用于模拟和分析电路中的不确定或高阻状态。这些符号帮助工程师识别电路中可能的问题,如竞争条件和浮动节点。
Contention: X
竞争状态(X) 表示电路试图将输出驱动到互相冲突的值(例如,1 和 0),导致输出无法确定。
- 特性:
- 实际输出值会在 0 和 1 之间浮动。
- 输出可能处于禁止区,或者根据环境条件(电压、温度、时间、噪声)而变化。
- 竞争状态通常导致过多的功耗,因为电路试图同时驱动不同的值。
- 应用:
- X 也常用来表示未初始化的值或在不关心(Don’t Care)条件下的输出。
- 警告:
- 竞争或未初始化的输出通常是电路设计中的 bug,需要仔细检查。
- 需要根据电路上下文来判断 X 的具体含义。
Floating: Z
浮动状态(Z) 表示输出处于高阻状态,节点被断开,电路呈现高阻抗。
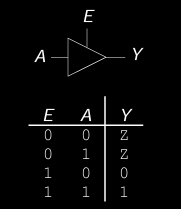
- 特性:
- 输出可能为 0、1 或在中间的任意值,取决于外部干扰。
- 浮动状态无法通过常规的电压表检测,因为节点没有确定的驱动源。
- 这种状态极易受外界物理接触或电磁干扰影响,导致输出随机变化。
- 实际例子:
- 例如在 三态缓冲器 中,当使能信号 \( E \) 为 0 时,输出 \( Y \) 处于浮动状态(Z);当使能信号为 1 时,输出根据输入 \( A \) 确定为 0 或 1。
E A Y 0 0 Z 0 1 Z 1 0 0 1 1 1
Tristate Buses
三态总线 利用浮动节点来允许多个驱动器连接到同一条总线,但确保在任意时间只有一个驱动器处于激活状态。
- 特性:
- 当一个驱动器激活时,其它所有驱动器处于高阻状态(Z),从而不会干扰总线上的数据传输。
- 三态总线常用于计算机系统中的共享资源,如处理器、存储器、以太网等设备,确保只有一个设备可以在某一时刻向总线写入数据。
Karnaugh Maps (K-Maps)
卡诺地图
Karnaugh图(K-Maps)是一种简化布尔表达式的图形工具,通过合并相邻的1来最小化布尔方程。这种方法特别适合3到4个变量的布尔表达式,使得逻辑电路的实现更加高效。
Karnaugh Maps 的概念
- K-Map 允许通过合并项来简化布尔表达式,减少不必要的逻辑门数量。
- 通过图形化的方式直观地表达和处理布尔表达式的最小化。
例如,对于表达式 \( PA + \overline{P}A = P \),Karnaugh图的使用可以清晰地显示合并的逻辑。
如何使用 K-Map
在 Karnaugh 图中,1 应该圈在相邻的方格中。对于布尔表达式,只包含那些在圈内 不同时存在 正常形式和补码形式的文字。
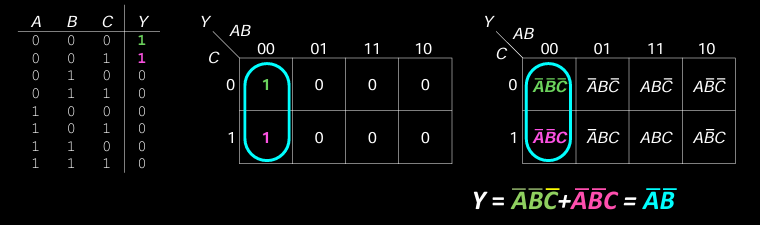
- 步骤:
- 在图中找到表示 1 的位置。
- 圈出相邻的1(在水平或垂直方向上,不能对角相邻)。
- 写出仅包含那些在圈中 不同时存在 正和反变量的文字的布尔表达式。
例如:
- 在 3 变量的真值表中,\( Y = \overline{A}BC + A\overline{B}C + AB\overline{C} \) 可以使用K-map进行简化。
Definitions and K-Map Rules
Key Definitions
- Complement: 在变量上方加横线表示补码,如 \( \overline{A}, \overline{B}, \overline{C} \),表示该变量的反值。
- Literal: 变量或其补码,例如 \( A, \overline{A}, B, \overline{B}, C, \overline{C} \)。
- Implicant: 字面量的乘积,如 \( AB\overline{C}, A\overline{C}, BC \),这些项在Karnaugh图中代表布尔方程的最小项。
- Prime Implicant: Karnaugh图中最大的圈,对应于最简表达式中最重要的项。这些项无法进一步合并。
K-Map 使用规则
- 每个 1 必须至少被圈一次:Karnaugh图中的每个 1 都应被包含在至少一个圈内。
- 每个圈必须跨越 2 的幂次方:圈内的方格数量必须是2、4、8等 2 的幂次方。例如,一个圈可以覆盖2个、4个、或8个格子,但不能覆盖3个或6个。
- 每个圈必须尽可能大:尽量合并更多的 1 以减少逻辑门的数量。
- 圈可以跨越边界:图的左、右边界,或上下边界是相连的,可以将相邻的1圈在一起。
4-Input K-Map 示例
在这个四输入变量的K-map中,输入变量为 \( A, B, C, D \),输出为 \( Y \)。
- Karnaugh图的每一个方格代表一个特定的输入组合。例如,\( AB = 00, CD = 00 \) 对应图的左上角,输出为1。
- 圈出相邻的1,得到的布尔表达式 \( Y \) 是这几个圈的组合。
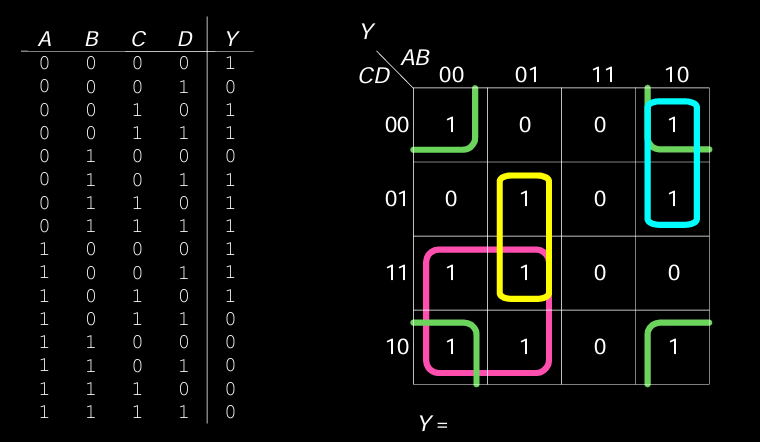
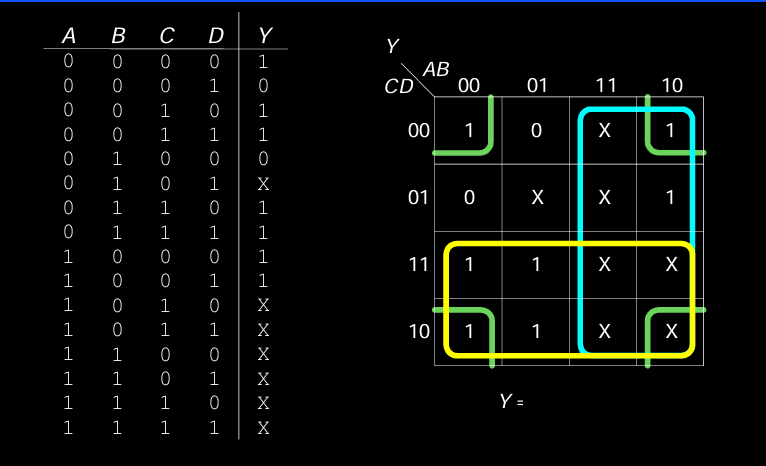
Karnaugh Maps with Don’t Cares
K-Map Rules Recap
- 每个 1 必须至少圈一次:任何在K-Map中的1必须被至少包括在一个圈内。
- 每个圈必须跨越 2 的幂次方:每个圈内的格子数必须是 2、4、8 等 2 的幂次方。
- 圈必须尽量大:圈应尽量包含更多的1,以简化表达式。
- 圈可以跨越边界:K-Map 的边界是相连的,所以可以跨越边界形成更大的圈。
- 仅当有助于简化方程时才圈 “don’t care” (X):”don’t care” 表示该输出的值对电路行为无关紧要,因此可以选择是否将其包含在圈中,以帮助简化布尔表达式。
示例:带有 “Don’t Care” 的 K-Map
在此例子中,\( A, B, C, D \) 作为输入,\( Y \) 作为输出,输出中包含一些 “Don’t Care”(X)。通过合理利用这些 “don’t care”,可以合并更多的1,从而减少逻辑门的数量并简化电路设计。
。。。
Combinational Building Blocks: Multiplexers
Multiplexer (Mux)
多路选择器(Mux)是一种常见的组合逻辑电路,它允许在多个输入之间进行选择并将选定的输入传递到输出。
- 选择:从 \( N \) 个输入中选择一个连接到输出。
- 选择输入:使用 \( \log_2 N \) 位的选择信号来控制输入。
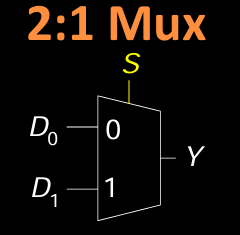
- 示例:2:1 Mux
在 2:1 多路选择器中,只有两个输入 \( D_0 \) 和 \( D_1 \),选择信号 \( S \) 决定哪个输入会连接到输出 \( Y \)。如果 \( S = 0 \),输出连接到 \( D_0 \);如果 \( S = 1 \),输出连接到 \( D_1 \)。
| S | D_1 | D_0 | Y |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
2:1 Multiplexer Implementations
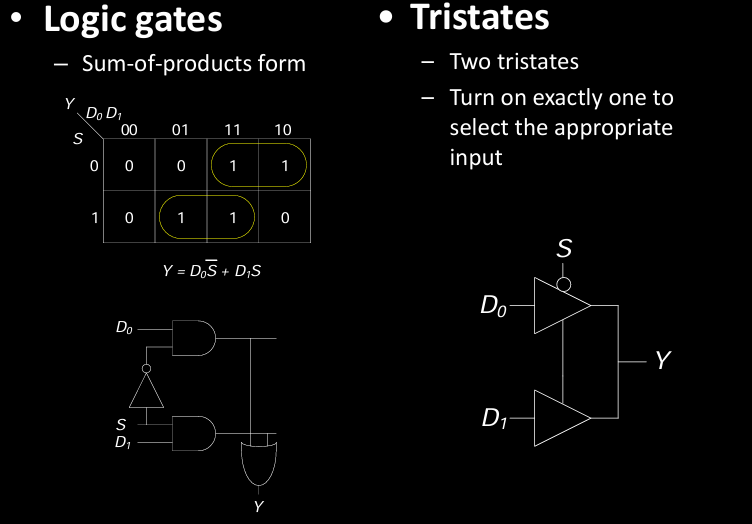
2:1 多路选择器有两种实现方式:
-
使用逻辑门: 这种方法采用 “乘积之和”(SOP)形式的布尔表达式。对于 2:1 Mux,输出 \( Y \) 的逻辑表达式为: \[ Y = D_0 \overline{S} + D_1 S \] 使用 AND 和 OR 门实现这个布尔表达式。
-
使用三态缓冲器:
- 使用两个三态缓冲器,其中每个缓冲器分别对应一个输入。当选择信号为 0 时,打开 \( D_0 \) 的三态缓冲器;当选择信号为 1 时,打开 \( D_1 \) 的三态缓冲器。
- 这样可以确保在任意时刻,只有一个输入连接到输出,防止信号冲突。
两种方法都有各自的优点,使用逻辑门更适合简单的组合电路,而三态缓冲器则在设计更复杂的电路中具有更好的灵活性。
4:1 Multiplexer Implementations
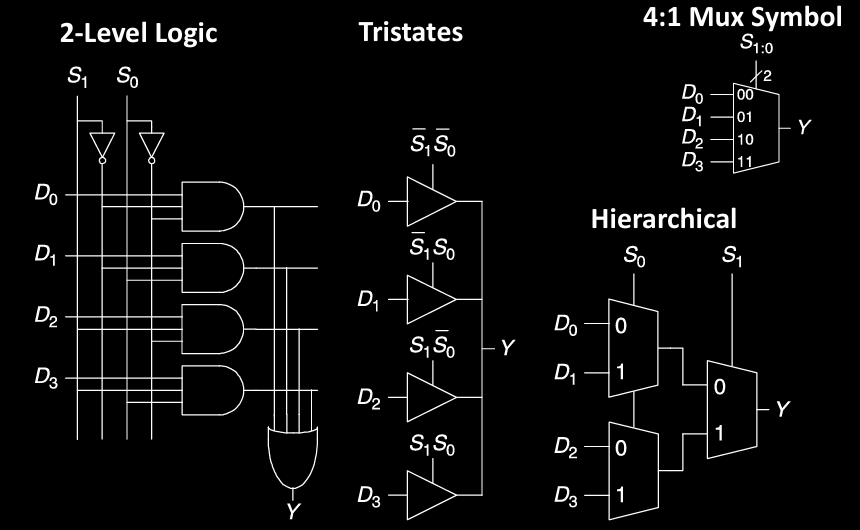
4:1 多路选择器(4:1 Mux)是一种常见的组合电路,能够从 4 个输入中选择一个输出。其实现方式包括不同的逻辑结构和符号表示。
实现方式
- 2-Level Logic:
- 使用 AND 和 OR 门实现。每个 AND 门结合选择信号 \( S_1 \) 和 \( S_0 \) 控制输入 \( D_0 \), \( D_1 \), \( D_2 \), \( D_3 \) 的传输。
- 选择信号 \( S_1 \) 和 \( S_0 \) 确定哪个输入将连接到输出 \( Y \)。
- 三态缓冲器(Tristates):
- 通过三态缓冲器控制每个输入信号的通过。选择信号 \( S_1 \) 和 \( S_0 \) 控制每个输入的三态缓冲器开启或关闭,从而选择一个输入信号 \( D_0 \) 至 \( D_3 \) 传递到输出。
- 仅允许一个输入在任意时刻接通输出,避免冲突。
- 4:1 Mux 符号表示:
- 这种表示法清楚地展示了选择信号和输入的关系。两个选择信号 \( S_1, S_0 \) 组合成 2 位的二进制数,用于选择哪个输入传递到输出 \( Y \)。
- 层次结构实现(Hierarchical):
- 使用两个 2:1 多路选择器(Mux)组合成 4:1 Mux。
- 选择信号 \( S_0 \) 决定哪个 2:1 Mux 输出有效,\( S_1 \) 决定选择的是哪一对输入信号。
Logic Using Multiplexers
使用 Mux 作为查找表(Lookup Table)
多路选择器也可以用作查找表(LUT),存储和生成布尔逻辑。通过将输入信号和选择信号组合,可以将任意布尔函数表示为多路选择器的输出。
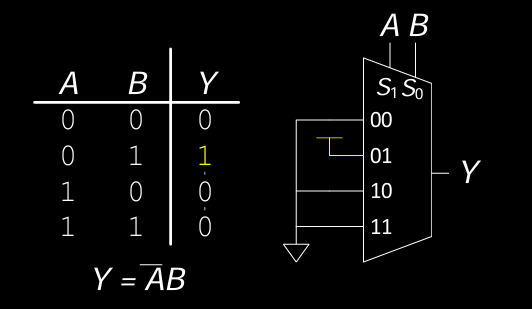
- 示例:给定一个 2 输入的逻辑表达式 \( Y = \overline{A}B \)。
- 表格列出输入信号 \( A \) 和 \( B \) 的所有组合及其对应的输出 \( Y \)。
- 通过将 \( A \) 和 \( B \) 作为选择信号 \( S_1, S_0 \),可以确定输出值。
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
通过这种方式,Mux 可以用于实现任何布尔函数,尤其是当作为查找表时,能够有效简化逻辑电路的设计。
Combinational Building Blocks: Decoders
Decoders
解码器(Decoder)是一个重要的组合电路模块,用于将 \( N \) 个输入解码为 \( 2^N \) 个独特的输出信号,每次只有一个输出为高电平(One-hot 输出),其余输出为低电平。这使得解码器在选择器、多路复用器、地址解码等场合中非常实用。

- 输入/输出:
- \( N \) 个输入信号,对应 \( 2^N \) 个输出信号。
- 例如,2:4 解码器有 2 个输入信号 \( A_1, A_0 \),可以产生 4 个输出 \( Y_3, Y_2, Y_1, Y_0 \)。
- 只有一个输出为高电平,其余输出为低电平。
-
真值表:
\( A_1 \) \( A_0 \) \( Y_3 \) \( Y_2 \) \( Y_1 \) \( Y_0 \) 0 0 0 0 0 1 0 1 0 0 1 0 1 0 0 1 0 0 1 1 1 0 0 0
Decoder Implementation
解码器的实现通常使用 AND 和 NOT 门。在2:4解码器中,输入信号 \( A_1 \) 和 \( A_0 \) 的不同组合通过 NOT 门和 AND 门的排列组合,选择相应的输出。
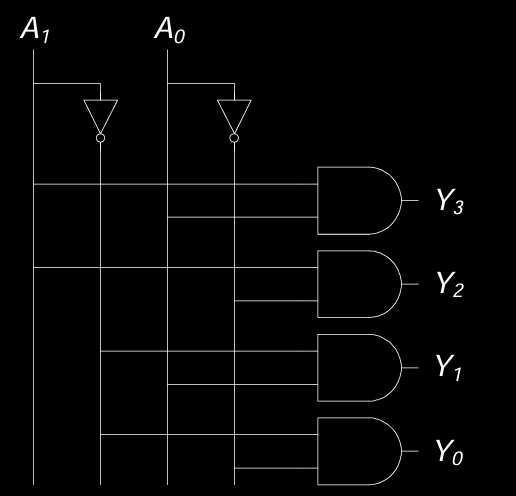
- \( Y_3 \) 输出的条件为:\( A_1 = 1 \) 和 \( A_0 = 1 \),即 AND 门会输出高电平。
- \( Y_0 \) 输出的条件为:\( A_1 = 0 \) 和 \( A_0 = 0 \),通过 NOT 门实现反转逻辑。
这种实现方式确保每次只有一个输出为高电平。
Logic Using Decoders
解码器也可用于实现布尔逻辑。通过解码输入信号,并将输出信号通过 OR 门组合,可以实现逻辑函数。解码器输出可以直接与布尔函数的最小项(minterm)对应。
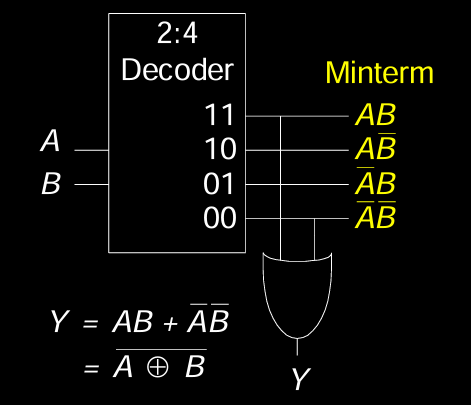
- 示例:
- 使用 2:4 解码器实现 \( Y = AB + \overline{A}·\overline{B} \),其逻辑表达式对应 XOR 逻辑函数 \( Y = \overline{A \oplus B} \)。
- 输入 \( A \) 和 \( B \) 通过解码器生成四个最小项,其中 \( AB \) 和 \( \overline{A}·\overline{B} \) 是感兴趣的项,将这两个输出通过 OR 门组合即可实现目标逻辑。
这种方式使得解码器可以高效地作为布尔函数生成的模块,在数字电路设计中非常常见。
Timing
Delay
电路中的延迟指的是输入信号发生变化到输出信号相应变化之间的时间间隔。延迟的主要来源是电路中的电容和电阻效应。延迟时间的减少是构建快速电路的关键,尤其是在高频数字电路设计中。
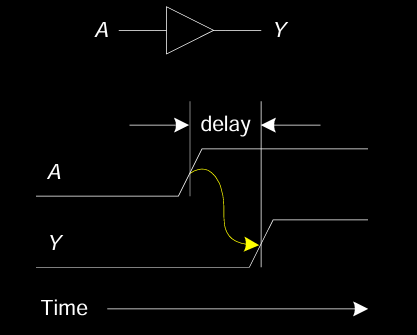
如图所示,当输入信号 \( A \) 发生变化时,输出信号 \( Y \) 并不会立即变化,而是存在一个短暂的延迟,直到输出稳定下来。
Propagation & Contamination Delay
传播延迟(Propagation Delay,\( t_{pd} \))
传播延迟是从输入信号发生变化到输出信号稳定的最长时间间隔。它是指输入信号变化后,输出完全稳定所需的最大延迟。
污染延迟(Contamination Delay,\( t_{cd} \))
污染延迟是从输入信号变化到输出信号最早可能发生变化的最短时间间隔。也就是说,输出信号开始响应输入变化的最小时间。
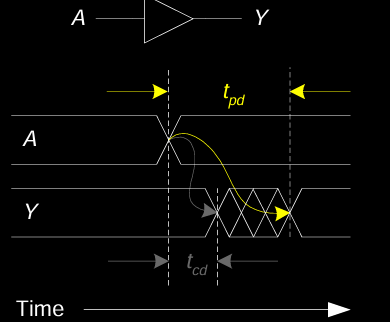
通过图示可以直观地看到,输入信号 \( A \) 改变后,输出信号 \( Y \) 并不会立即达到稳定状态,而是在污染延迟时间 \( t_{cd} \) 之后开始波动,并最终在传播延迟 \( t_{pd} \) 结束时达到稳定状态。
Propagation & Contamination Delay的原因
延迟的产生原因包括电路中的电容、电阻,以及光速限制等物理因素。
传播延迟 \( t_{pd} \) 和污染延迟 \( t_{cd} \) 可能不同的原因有以下几点:
- 上升和下降延迟不同:电路中高电平(1)到低电平(0)的转换时间,和低电平(0)到高电平(1)的转换时间可能不对称。
- 多输入和多输出:有些输入和输出信号可能比其他信号传播得更快。
- 温度影响:电路在高温环境下通常速度较慢,而在低温下则运行较快。
了解这些延迟特性对于优化电路设计、提高运行速度和稳定性至关重要。
Critical (Long) & Short Paths
电路中的关键路径是信号从输入传播到输出所经过的最长延迟路径。电路的总延迟主要由关键路径决定。而短路径则是信号经过的最短延迟路径。理解这些路径对于优化电路性能至关重要。
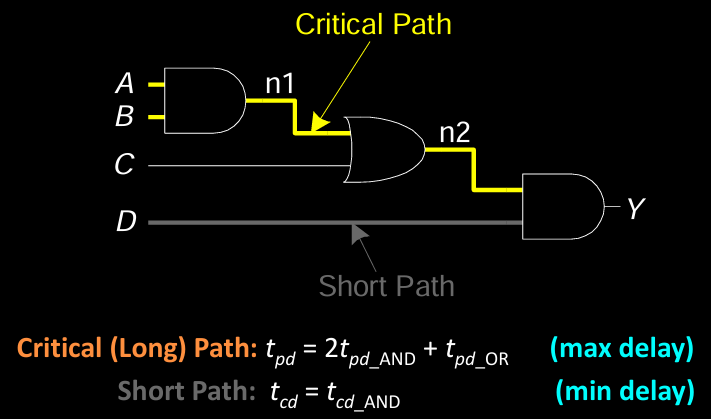
- 关键路径 (Critical Path):是最大延迟路径,影响电路的最大速度。例如图中信号从 \( A, B \) 经由 \( n1 \) 和 \( n2 \) 到达输出 \( Y \),传播延迟为 \( t_{pd} = 2t_{pd AND} + t_{pd OR} \)。
- 短路径 (Short Path):是信号传播的最小延迟路径。例如信号从 \( C, D \) 经由一个 AND 门到达输出 \( Y \),其污染延迟为 \( t_{cd} = t_{cd_AND} \)。
最大延迟和最小延迟的差异可以影响电路的同步性,如果差异过大,可能会导致计时错误。
Glitches(毛刺)
毛刺是指当输入信号发生单次变化时,输出信号由于不同路径的传播延迟而可能出现短暂的、不预期的多次变化现象。毛刺通常是由多路径传播延迟不同步造成的,它会导致输出信号在稳定之前短暂的抖动。
Glitch Example
在此示例中,当 \( A = 0 \),\( C = 1 \),并且 \( B \) 由 1 变为 0 时,观察输出 \( Y \) 会发生什么。
- 初始电路为 \( Y = \overline{A}B + BC \),其中 AND 门和 OR 门负责处理输入信号 \( A \),\( B \),\( C \)。
- 当 \( B \) 下降时,信号会通过不同的路径到达输出 \( Y \),其中较长的关键路径 \( n1 \) 需要更多时间传播,而较短的路径 \( n2 \) 则较快传递。
- 由于路径延迟的差异,输出 \( Y \) 在短时间内会发生抖动,产生毛刺现象。
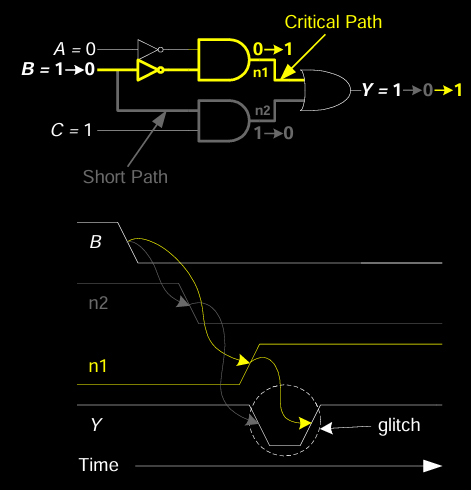
如图所示,电路中的关键路径 \( n1 \) 经过两个逻辑门(AND 和 OR),而短路径 \( n2 \) 只经过一个逻辑门(OR)。在 \( B \) 信号变化时,短路径先更新,而关键路径由于延迟较长,导致输出 \( Y \) 在信号稳定之前产生了短暂的毛刺。
Fixing the Glitch
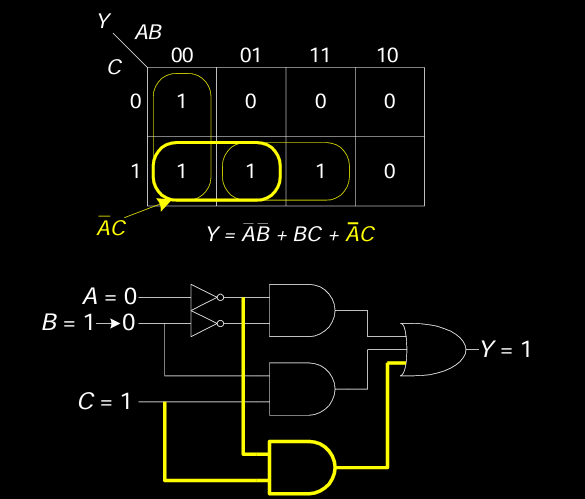
通过修改电路逻辑,可以减小或消除毛刺。使用卡诺图分析,可以优化表达式 \( Y = \overline{A}\overline{B} + BC + \overline{A}C \),并对电路进行改进,从而消除毛刺问题。图中通过优化后的卡诺图给出了解决方案,并将相应的逻辑门电路调整为更加稳定的配置。
Why Understand Glitches?
理解毛刺现象非常重要,尤其是在同步设计中。由于同步设计会使用时钟信号,因此很多情况下毛刺不会引发严重问题。然而,在某些情况下,识别并修复毛刺是至关重要的,特别是在仿真或示波器检测中。
需要注意的是,不能完全消除所有毛刺。当多个输入同时发生变化时,即使经过优化的设计仍然可能产生毛刺,因此需要根据具体的电路应用场景进行合理的优化与处理。
