Chapter 3: Sequential Logic Design
《Digital Design and Computer Architecture: RISC-V Edition》
在数字设计与计算机体系结构中,时序逻辑设计(Sequential Logic Design)是一个关键概念,它与组合逻辑不同,后者的输出只依赖于当前的输入。而顺序逻辑的输出不仅取决于当前输入,还取决于之前的输入,这一特性使其能够具有记忆功能。通过这种记忆功能,顺序逻辑能够保存状态,并根据外部信号的变化进行决策。这是大多数现代计算机系统和电子设备的核心工作原理。
本章将详细探讨时序逻辑设计的各个方面,介绍其基本构建模块——状态元件,并阐述如何通过这些元件构建同步时序逻辑和有限状态机(Finite State Machines, FSMs)。另外,章节内容还涵盖了顺序逻辑的时序分析,探讨时钟偏斜、同步化及并行性等问题。
Chapter 3: Topics
1. 状态元件(State Elements)
状态元件是时序逻辑设计的基础,负责存储和维持电路的状态。本节将介绍不同类型的状态元件,包括:
- 双稳态电路(Bistable Circuit):最简单的存储元件,具有两个稳定状态。
- SR锁存器(SR Latch):通过两个输入控制设定(Set)和复位(Reset)的简单存储单元。
- D锁存器(D Latch):在时钟信号的作用下进行数据的存储。
- D触发器(D Flip-Flop):在时钟边沿捕获输入信号的状态元件,用于同步电路设计。
- 状态元件的变种(Variations):探讨不同锁存器和触发器的变种及其应用。
2. 同步时序逻辑(Synchronous Sequential Logic)
同步时序逻辑是使用时钟信号控制状态变化的电路设计方法,确保系统的所有部分都根据统一的时钟信号进行协调。这部分内容将详细解释同步电路的工作原理及其优势。
3. 有限状态机(Finite State Machines)
有限状态机是时序逻辑电路的一个重要应用,通过定义状态和状态转移规则来控制系统行为。本节将介绍以下几种状态机模型:
- 摩尔状态机(Moore FSM):输出只与当前状态有关的状态机。
- 米利状态机(Mealy FSM):输出不仅与当前状态有关,还取决于当前输入。
- 分解状态机(Factored FSM):将复杂状态机分解为多个较小的状态机,简化设计。
4. 顺序逻辑的时序分析(Timing of Sequential Logic)
时序分析是时序逻辑设计中至关重要的一环,它决定了电路的正确性和速度。时钟信号的偏斜(Clock Skew)和信号的同步化(Synchronization)是时序分析中的两个重要问题。本节将讨论如何在设计中应对这些挑战。
5. 并行性(Parallelism)
现代系统中,并行计算和数据处理已成为提高性能的关键手段。在时序逻辑设计中,并行性可以通过多种方法实现,减少时延并提高计算效率。
Sequential Logic - State Elements
状态元件
顺序逻辑的输出依赖于当前的输入和之前的输入值,这一特性使得顺序逻辑具备记忆功能。与组合逻辑不同,时序逻辑电路中的状态会随着时间的推移而发生变化,从而能够处理更复杂的任务,例如计数器、寄存器、甚至是复杂的控制系统。理解状态元件是理解整个时序逻辑设计的第一步。
Sequential Circuits
时序电路是一类能够对事件赋予顺序的电路。与组合逻辑电路不同,时序电路具有短期记忆能力,它可以记住之前的输入状态,并将输出反馈回输入端来存储信息。这一反馈机制使时序电路能够根据先前的状态及当前的输入做出决定,广泛应用于寄存器、计数器和状态机等。
时序电路的核心功能包括:
- 赋予事件顺序:使电路能够按照时序依次处理数据。
- 具有短期记忆:能记住之前的输入状态,这种记忆通常是暂时的。
- 使用反馈机制:通过将输出反馈到输入来存储和保持状态。
State Elements
在时序电路中,状态元件用于存储和维持电路的状态。状态代表的是与之前输入相关的所有信息,这些信息足以预测电路的未来行为。通常,状态元件存储的信息量较少,比如一个位元(bit),它存储的是之前捕获的最后一个值。
典型的状态元件包括:
- 双稳态电路(Bistable Circuit):这是最基础的状态元件,能存储两个稳定状态。
- SR锁存器(SR Latch):通过输入的设定(Set)和复位(Reset)来控制存储状态。
- D锁存器(D Latch):存储数据,通常由时钟信号控制。
- D触发器(D Flip-Flop):在时钟边沿触发时存储输入数据。
这些状态元件的主要任务是存储状态,并在时序电路的操作过程中保持和更新这些状态。
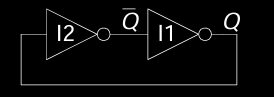
Bistable Circuit
双稳态电路
双稳态电路是所有其他状态元件的基本构建模块,它具有两个输出:Q 和 Q̅(Q的反相),没有外部输入。双稳态电路可以稳定在两个不同的状态(0或1),并通过反馈保持在某一个状态上,直到一个外部的触发事件导致状态的切换。这种电路的简单结构和可靠性使其成为存储位元信息的基础。
Bistable Circuit Analysis
双稳态电路可以通过分析其两种可能状态来理解其工作原理。根据输出Q的值,电路可以处于以下两种情况之一:
- 当 Q = 0 时:
- 电路处于一种状态,输出
Q为0,Q̅为1。 - 这种状态会通过电路中的反馈机制保持不变,直到外部条件变化。
- 电路处于一种状态,输出
- 当 Q = 1 时:
- 电路处于另一种状态,输出
Q为1,Q̅为0。 - 这一状态同样会通过反馈回路保持稳定,直到发生切换。
- 电路处于另一种状态,输出
通过这种分析,可以看出双稳态电路是如何通过反馈机制来稳定在两个状态之一,从而存储一个位的信息。这种电路的特性使其成为构建锁存器、触发器等更复杂状态元件的基础。
SR Latch
SR锁存器
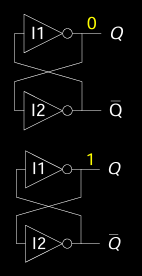
SR锁存器(Set/Reset Latch)是一种基础的存储元件,广泛用于时序逻辑电路中。它可以通过两个输入端S(Set)和R(Reset)来控制输出的状态,并具有记忆功能。SR锁存器的主要任务是存储一个位元的信息,这个信息可以是设定状态或复位状态,并保持不变,直到输入发生变化。
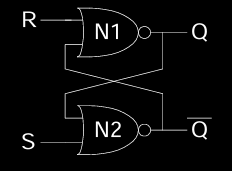
SR锁存器是双稳态电路的具体实现形式,它使用两个交叉耦合的逻辑门(通常为NAND门或NOR门)来构成。这些逻辑门形成一个反馈环路,确保输出状态能够维持在设定值。
SR Latch Structure
SR锁存器的核心结构如图所示,由两个逻辑门N1和N2构成。输入端S用于设定输出,而输入端R用于复位输出。SR锁存器的输出为Q和Q̅(Q的反相),通过交叉反馈,这些输出状态能保持稳定。
Four Possible Input Cases
根据输入S和R的不同组合,SR锁存器可以有四种可能的状态:
- S = 1, R = 0(设定):
-
当
S = 1且R = 0时,锁存器进入设定状态,输出Q = 1,Q̅ = 0。这意味着SR锁存器已存储1的状态。
-
- S = 0, R = 1(复位):
-
当
S = 0且R = 1时,锁存器进入复位状态,输出Q = 0,Q̅ = 1。此时,SR锁存器存储了0的状态。
-
- S = 0, R = 0(保持):
-
当
S = 0且R = 0时,锁存器保持当前状态,输出保持不变。如果之前输出为Q = 1,则仍然为Q = 1,如果之前为Q = 0,则保持Q = 0。这是SR锁存器的记忆功能,它能够维持之前的状态。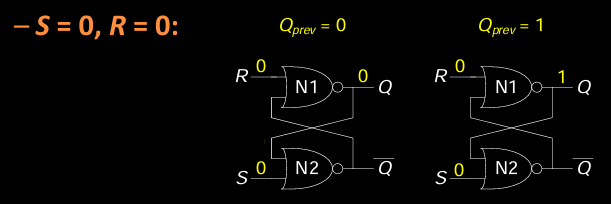
-
- S = 1, R = 1(无效状态):
-
当
S = 1且R = 1时,锁存器进入无效状态,因为Q和Q̅同时为1违反了电路的逻辑关系。这种情况应当避免。
-
SR Latch Analysis
Case 1: S = 1, R = 0
当S = 1且R = 0时,锁存器会进入设定状态,输出Q = 1,Q̅ = 0。逻辑门N1的输出为0,N2的输出为1,反馈回路确保锁存器维持这一状态。
Case 2: S = 0, R = 1
当S = 0且R = 1时,锁存器进入复位状态,输出Q = 0,Q̅ = 1。这种情况下,N1输出1,N2输出0,电路保持该复位状态。
Case 3: S = 0, R = 0
当S = 0且R = 0时,SR锁存器进入保持状态,保持之前的输出状态。如果之前Q = 0,那么输出保持为0;如果之前Q = 1,则保持为1。这一状态展现了SR锁存器的记忆功能。
Case 4: S = 1, R = 1
当S = 1且R = 1时,SR锁存器进入不稳定状态,因为Q和Q̅都被驱动为1,这是一种无效状态。为了避免这一情况,电路设计必须确保输入S和R不会同时为1。
SR Latch Functionality
- 设定状态(Set):当
S = 1, R = 0时,锁存器输出Q = 1。 - 复位状态(Reset):当
S = 0, R = 1时,锁存器输出Q = 0。 - 保持状态(Memory):当
S = 0, R = 0时,锁存器保持之前的输出状态。 - 无效状态:当
S = 1, R = 1时,锁存器进入无效状态,需避免此输入组合。
设计电路时,必须确保输入信号不会同时触发设定和复位操作,以防止无效状态的出现。这通常通过额外的逻辑电路进行防护。
D Latch
D锁存器
D锁存器(D Latch)是一种常用的时序逻辑电路元件,它通过时钟信号和数据输入来控制输出。D锁存器的设计旨在解决SR锁存器在输入信号S和R同时为1时出现的无效状态问题。通过将输入简化为单个数据输入D,D锁存器确保了其在任何输入条件下都能正常工作。
D锁存器具有两个输入:
- 时钟信号(CLK):控制输出何时发生变化。只有当时钟信号有效时,D锁存器才会根据输入数据
D改变输出。 - 数据输入(D):决定输出的状态,即输出
Q将随D输入而改变。
当时钟信号为高电平时,D锁存器将根据数据输入D的值改变输出。当时钟信号为低电平时,输出保持不变。这样可以确保在时钟信号的控制下,电路同步地存储和更新数据。
D Latch Internal Circuit
D锁存器的内部电路结构包括两个逻辑门和一个反相器。其主要工作过程如下:
- 当时钟信号为高时,数据输入
D决定了锁存器的输出。如果D = 1,则输出Q = 1;如果D = 0,则输出Q = 0。 - 当时钟信号为低时,锁存器保持之前的输出状态,不受数据输入的影响。
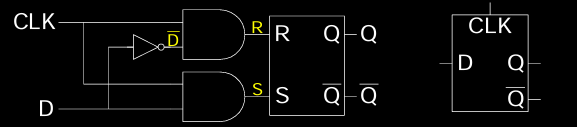
D锁存器的电路图展示了输入CLK和D如何通过交叉连接的RS锁存器来控制输出。这里的S和R信号由数据输入D和其反相信号D̅生成,这种结构使得锁存器能够根据D的值设置或复位输出。
D Latch Functionality Table
D锁存器的功能可以通过一个真值表来表示,展示了不同输入条件下的输出变化:
| CLK | D | D̅ | S | R | Q | Q̅ |
|---|---|---|---|---|---|---|
| 0 | X | X | 0 | 0 | Qprev | Qprev̅ |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 |
从表中可以看出:
- 当时钟信号
CLK = 0时,输出保持不变,即Q保持其先前的状态(Qprev)。 - 当时钟信号
CLK = 1时,输出取决于数据输入D。如果D = 0,输出Q = 0;如果D = 1,输出Q = 1。
通过这种设计,D锁存器能够在时钟信号的控制下有效地存储数据,并避免了SR锁存器的无效状态问题。
D Flip-Flop
D触发器
D触发器(D Flip-Flop)是时序逻辑设计中一种重要的状态元件,主要用于时钟驱动的同步电路。与D锁存器(D Latch)不同,D触发器仅在时钟信号的特定边沿(上升沿或下降沿)采样输入数据,并将其存储在输出中。这种特性使得D触发器适用于需要高精度时序控制的电路,如寄存器、计数器和有限状态机(FSM)。
D触发器有两个主要输入:
- CLK(时钟信号):控制数据何时从输入采样到输出。D触发器只在时钟的边沿(通常是上升沿)更新输出。
- D(数据输入):控制要存储的数据。D触发器在时钟信号触发时,将数据输入的值传递到输出。
D Flip-Flop Internal Circuit
D触发器的内部结构由两个背靠背连接的D锁存器(L1和L2)组成,它们分别由互补的时钟信号控制。其基本工作机制如下:
- 当 CLK = 0 时:
- 第一个D锁存器L1处于活动状态,输入
D的数据通过L1锁存,但不会立即传递到输出Q。 - 第二个D锁存器L2则处于锁定状态,不会更新输出。
- 第一个D锁存器L1处于活动状态,输入
- 当 CLK = 1 时:
- 第一个D锁存器L1锁定当前状态,不再接受输入数据。
- 第二个D锁存器L2激活,将L1存储的数据传递到输出
Q。
通过这种方式,D触发器只在时钟信号的边沿更新输出,确保数据同步且稳定。这种级联的设计使得D触发器能够防止信号传播时的亚稳态问题,提高了电路的时序控制能力。
D Latch vs. D Flip-Flop
D锁存器和D触发器虽然都依赖于时钟信号和数据输入,但它们的行为在时序控制上有着显著的差异:
- D锁存器:
- D锁存器在时钟信号为高电平时(而非特定边沿)会根据输入数据
D更新输出Q。 - 这种特性意味着D锁存器在时钟信号为高的整个持续时间内都是透明的,即输入
D直接控制输出。
- D锁存器在时钟信号为高电平时(而非特定边沿)会根据输入数据
- D触发器:
- D触发器则只在时钟信号的边沿(通常是上升沿)更新输出。它在时钟信号的非边沿期间锁定输出,避免了数据的意外更改。
- 这种特性使得D触发器更加适合复杂时序要求的设计,尤其是在需要精确同步的情况下。
D锁存器在时钟信号为高时会立即响应数据输入,而D触发器则仅在时钟的上升沿捕获数据并更新输出。这使得D触发器比D锁存器更加适合同步时序的电路设计。
Variations on a Flip-Flop
触发器的变体
Registers: One or More Flip-Flops 寄存器:一个或多个触发器
寄存器是由多个触发器组成的时序逻辑电路,用于存储数据。每个触发器存储一位数据,多个触发器可以组合在一起形成一个多位寄存器。图中展示了一个4位寄存器,由四个D触发器组成,每个触发器存储一位数据(Q0到Q3)。当时钟信号(CLK)触发时,4位数据从输入(D0到D3)被同时存储到寄存器中,并通过相应的输出端(Q0到Q3)输出。
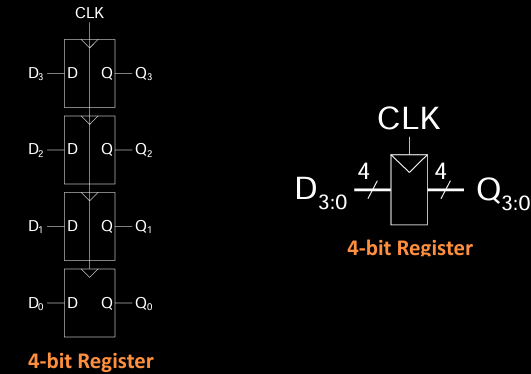
寄存器在计算机系统中广泛应用,用于暂时存储处理器中的数据或指令。通过这种并行存储结构,寄存器可以同时处理多位数据,提升处理效率。
Enabled Flip-Flops
使能型触发器(Enabled Flip-Flops)是在普通D触发器基础上增加了一个使能输入端(EN),用来控制何时存储新数据。它的工作机制如下:
- 输入信号:使能型触发器有三个输入端,分别是时钟信号
CLK、数据输入D、和使能信号EN。 - 功能:
- 当 EN = 1 时:触发器在时钟信号的边沿采样输入数据
D,并将其存储在输出端Q。 - 当 EN = 0 时:触发器忽略输入数据,不更新输出,保持之前的状态。
- 当 EN = 1 时:触发器在时钟信号的边沿采样输入数据
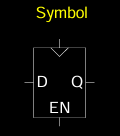
这种设计允许在需要时存储数据,并在不需要时保持输出稳定,广泛用于需要有条件存储的场景,例如控制信号或计数器的启用。
Resettable Flip-Flops
可复位触发器(Resettable Flip-Flops)是一种带有复位功能的D触发器,能够在特定情况下强制将输出复位为0。它具有三个输入:
- 时钟信号(CLK):控制数据存储的时序。
- 数据输入(D):控制输出的值。
- 复位输入(Reset):用于控制触发器复位。
功能:
- 当 Reset = 1 时:无论数据输入为何,输出
Q被强制设定为0。 - 当 Reset = 0 时:触发器按照正常D触发器的方式工作,根据时钟信号采样数据输入
D并更新输出。
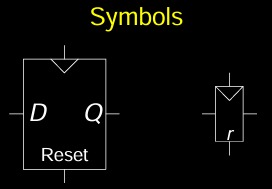
这种复位功能非常有用,尤其在系统初始化或异常恢复时,可以通过复位输入快速将电路状态归零。
Resettable Flip-Flops
Two Types of Resettable Flip-Flops
复位型触发器可以根据系统需求,分为同步和异步两种类型:
-
同步复位:复位操作与时钟信号同步,只有在时钟信号边沿时,复位信号才会生效,控制电路的状态改变。这种复位方式有助于确保整个系统的时序一致性。
-
异步复位:复位操作不依赖于时钟信号,可以在任意时刻激活复位信号,从而立即将电路状态强制设定为0。这种复位方式响应速度快,常用于系统的快速重置。
Settable Flip-Flops
设定型触发器(Settable Flip-Flops)是另一个常见的触发器变体,它的输入包括时钟信号CLK、数据输入D和设定输入Set。与复位型触发器类似,设定型触发器能够强制将输出设定为1,具体功能如下:
- Set = 1:无论数据输入
D为何,输出Q被强制设定为1。 - Set = 0:触发器按照正常的D触发器行为,根据时钟信号和数据输入进行正常操作。
这种设定功能常用于需要快速将系统状态置为1的场景,特别是在电路启动或初始化时。
Synchronous Sequential Logic
同步时序逻辑(Synchronous Sequential Logic)是时序电路设计中最常见的形式,所有状态的改变都由时钟信号驱动。时钟信号为同步电路提供了一个统一的时间基准,确保所有逻辑操作在固定的时序下发生。
Sequential Circuits
时序电路包含所有非组合逻辑电路,它们依赖于当前输入以及之前的状态来决定输出。这些电路通常包括反馈路径,将输出部分重新输入到电路中,形成一个闭环结构,使得电路能够存储状态。
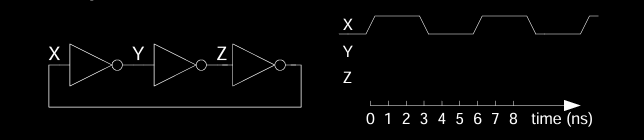
在时序电路中,有一个经典的问题电路示例:由三个反相器组成的电路(如图所示),形成一个环路。这个电路的输出反复在0和1之间切换,导致电路振荡。其特征包括:
- 无输入,仅通过反馈实现自驱动。
- 振荡电路,因为其没有稳定的状态,不断在0和1之间切换。
- 振荡周期取决于反相器的延迟时间。
- 循环路径:电路的输出反馈回输入,形成一个闭环。
这种电路的振荡行为展示了时序电路中的一种不稳定状态,因此设计者需要谨慎处理具有循环路径的电路,确保系统的稳定性。
Synchronous Sequential Logic Design
同步时序逻辑设计通过插入寄存器来打破循环路径,确保电路中的状态变化与时钟信号同步。寄存器在系统中保存状态,并且在时钟信号的边沿发生变化时,更新系统状态。同步电路中,时钟信号确保系统的所有部分都按照统一的时间基准运作。
同步时序电路设计的关键规则
- 每个电路元件要么是一个寄存器,要么是组合逻辑电路。
- 至少有一个电路元件是寄存器,用来存储状态。
- 所有寄存器都接收相同的时钟信号,确保全系统同步。
- 每条循环路径中至少包含一个寄存器,用来打破无终止的反馈循环。
常见的两种同步时序电路:
- 有限状态机(Finite State Machines,FSMs)
- 流水线(Pipelines)
FSMs: Finite State Machines
有限状态机
有限状态机(FSM)是同步时序电路的一种重要类型,用于根据当前状态和输入决定下一状态。FSM包括两个主要组成部分:
- 状态寄存器:用于存储当前的状态信息。每次时钟边沿触发时,状态寄存器根据组合逻辑电路的输出更新其状态。
- 组合逻辑:根据当前状态和输入计算下一状态和输出。
FSM中的状态和输出由当前状态和输入共同决定,这种设计使得FSM能够实现复杂的控制逻辑,用于许多自动控制和决策系统中。
Finite State Machines (FSMs) Operation
FSM的下一个状态由当前状态和输入决定。这意味着FSM的行为在每个时钟周期都会根据系统的当前状态和外部输入发生变化,从而实现预定的状态转移和逻辑操作。
这种状态机模型广泛用于数字系统中,如CPU控制单元、协议控制器、自动售货机等,能够通过有限的状态实现复杂的行为。
Next State Determination
有限状态机(FSM)的下一个状态由当前状态和输入决定。FSM有两种主要类型,它们在输出逻辑上有所不同:
- 摩尔状态机(Moore FSM):输出仅依赖于当前状态,与输入无关。
- 米利状态机(Mealy FSM):输出依赖于当前状态和输入的组合。
Moore FSM
在Moore状态机中,输出完全由当前状态决定。由于输出与输入无关,这种设计通常简化了输出逻辑的复杂度,但可能导致状态转移过程稍慢,因为每次输出改变都必须等待状态更新。
Mealy FSM
在Mealy状态机中,输出同时依赖于当前状态和输入。这意味着Mealy FSM在状态改变之前,可以基于输入产生输出。因此,Mealy FSM往往响应更快,但输出逻辑的复杂性增加。
FSM Design Procedure
设计FSM的过程分为以下几个步骤:
-
识别输入和输出:确定哪些信号将作为状态机的输入,以及它应产生的输出信号。
-
绘制状态转移图:根据系统需求绘制状态转移图,显示不同状态之间的转移路径。
- 编写状态转移表和输出表:
- 对于Moore FSM,状态转移表和输出表是分开的,因为输出仅依赖于当前状态。
- 对于Mealy FSM,状态转移表和输出表是合并的,因为输出同时依赖于状态和输入。
-
选择状态编码:为每个状态分配一个唯一的二进制编码,以便在硬件中实现这些状态。
-
重写状态转移表和输出表,应用状态编码:将原始的状态转移表和输出表转换为使用状态编码的表格。
-
编写下一状态和输出逻辑的布尔方程:通过分析状态转移表,得出控制状态转移和输出的布尔方程。
- 绘制电路原理图:最后,根据设计的布尔逻辑和状态表,绘制FSM的具体电路实现图。
这一设计过程系统化地将高层次的状态机模型转换为具体的硬件实现,确保系统按预期工作。
Moore FSM Example
FSM Example: Traffic Light Controller
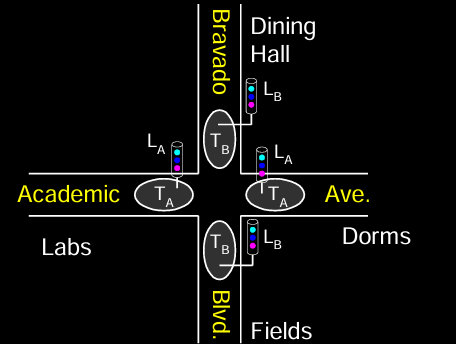
这个摩尔状态机(Moore FSM)例子展示了一个交通灯控制器的设计。在此交通控制系统中:
- 交通传感器:
T_A和T_B,用于检测两个道路方向上是否有交通流量。当传感器检测到有交通时,信号为TRUE。 - 交通灯:
L_A和L_B,分别控制两条路的红绿灯。状态机根据交通传感器的输入决定交通灯的状态。
FSM的功能是根据各方向的交通情况控制交通灯的变化,以确保交通顺畅且安全。
FSM Black Box
这个FSM被看作一个黑箱模型,其输入和输出定义如下:
- 输入:
- CLK:时钟信号,控制状态机的时序。
- Reset:复位信号,用于初始化系统,将FSM重置到初始状态。
- T_A 和 T_B:来自交通传感器的输入,表明两条道路上的交通情况。
- 输出:
- L_A 和 L_B:控制对应道路的交通灯信号。
通过这些输入,FSM控制交通灯的状态变化,确保交通信号根据当前状态和传感器输入适当转换。
FSM State Transition Diagram
在摩尔状态机中,输出与状态相关,输出标记在每个状态内部。FSM的状态转移图展示了系统的状态如何根据输入信号转移:
- 状态(States):用圆圈表示,每个状态对应一种交通灯配置。例如,状态
S0表示L_A为绿色、L_B为红色。 - 状态转移(Transitions):用弧线表示,指示在特定输入条件下如何从一个状态转移到另一个状态。
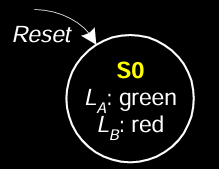
图中的状态S0代表系统的初始状态,交通灯L_A为绿灯,L_B为红灯。当某些条件满足时,FSM会根据传感器输入进行状态转换,从而控制交通灯的变化。
FSM State Transition Table
状态转移表展示了有限状态机(FSM)如何在不同输入条件下从一个状态转移到下一个状态。对于交通灯控制系统,当前状态S和传感器输入T_A、T_B决定了下一个状态S':
- 当前状态(S):表示系统当前的状态,例如
S0、S1等。 - 输入(T_A, T_B):表示检测到的交通流量,
T_A和T_B分别对应两个方向上的交通传感器。 - 下一个状态(S’):根据当前状态和输入决定的下一个状态。
例如,当系统处于S0状态并且T_A=0时,FSM将转移到S1状态。
FSM Encoded State Transition Table
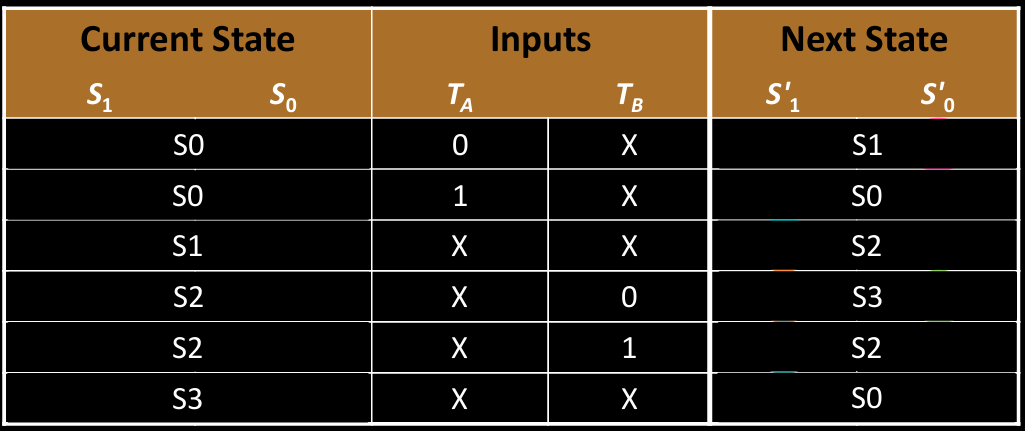
状态转移表经过编码后,显示了当前状态和下一状态的二进制编码:
- 状态编码:每个状态(
S0,S1,S2,S3)都有唯一的二进制编码,如S0为00,S1为01,S2为10,S3为11。 - 输入:传感器输入
T_A和T_B决定了下一个状态的变化。 - 下一状态编码:根据当前状态和输入,计算出下一状态的编码。
例如,当前状态S0(00)在T_A=1时,将转移到S1(01)。
FSM Output Table
输出表显示了每个状态下交通灯的输出配置:
- 当前状态:使用二进制编码表示,例如
S0对应00。 - 输出(L_A1, L_A0, L_B1, L_B0):控制两个方向的交通灯,
L_A表示方向A的灯光状态,L_B表示方向B的灯光状态。可能的灯光状态包括绿灯、黄灯和红灯,分别用二进制表示,如:- 绿灯:
00 - 黄灯:
01 - 红灯:
10
- 绿灯:
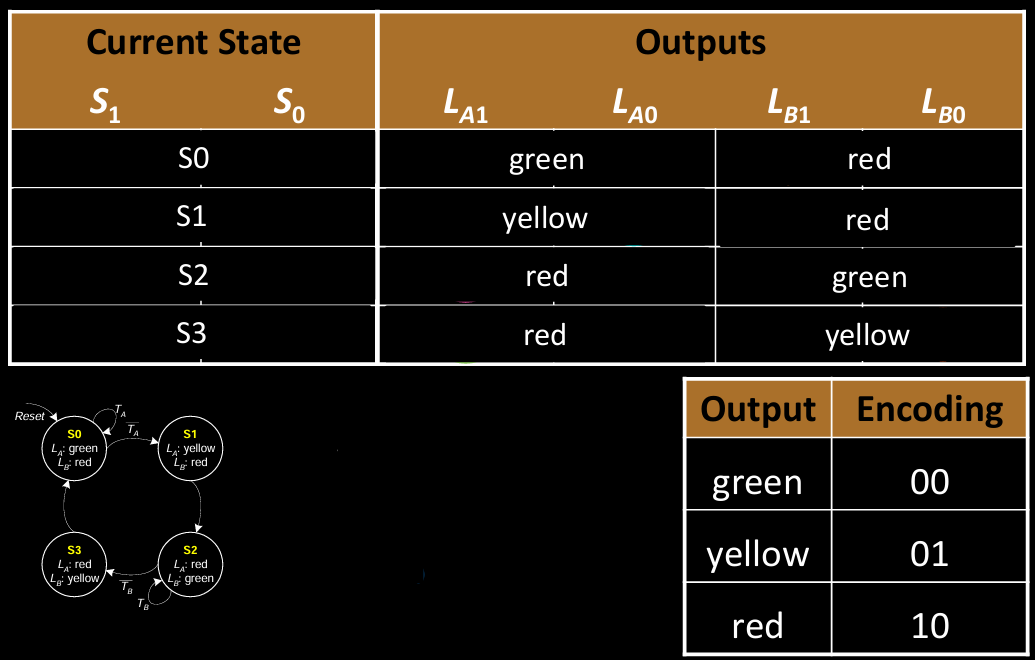
例如,状态S0对应的灯光配置为L_A为绿灯,L_B为红灯。
FSM Timing Diagram
时序图展示了有限状态机(FSM)在时钟周期中的行为,说明了系统状态、输入和输出信号的变化如何随时间演变。
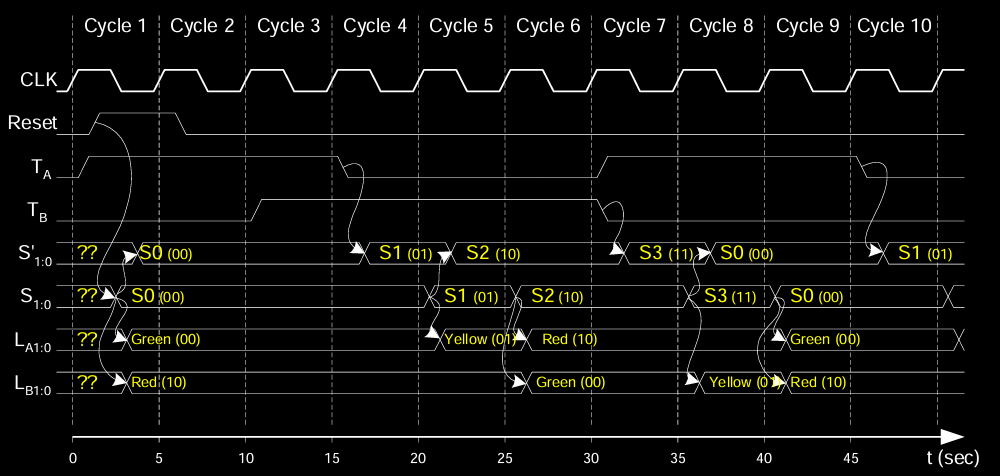
- 时钟信号(CLK):时钟信号驱动状态机的变化。在每个时钟周期的边沿,FSM根据当前状态和输入信号决定下一个状态。
- 复位信号(Reset):复位信号在系统启动时将状态机初始化为默认状态。在这个交通灯控制系统中,复位信号将FSM设置为
S0状态,即方向A的绿灯,方向B的红灯。 - 传感器输入(T_A, T_B):检测不同方向的交通状况。在时序图中,这些输入信号触发状态转移,影响交通灯的变化。
- 状态(S1, S0):展示了FSM如何在不同的时钟周期根据输入信号从一个状态转移到另一个状态。在图中,状态从
S0(00)到S1(01)再到S2(10)的转移过程显示了每个时钟周期内的变化。 - 输出信号(L_A, L_B):控制交通灯的状态。时序图展示了交通灯在各个时钟周期中如何变化,例如从绿灯切换到黄灯再切换到红灯。
时序图的目的是帮助理解FSM的操作和状态切换过程,确保设计的状态机能按照预期工作。
State Encodings
在设计有限状态机时,状态编码是一个关键步骤,用于将每个状态表示为唯一的二进制编码。常见的编码方式包括:
- 二进制编码:每个状态用尽可能少的位来编码,这种方式适用于状态数较少的情况。
- One-hot编码:每个状态使用多个位表示,其中只有一个位为1,其余位均为0。这种方式在状态数较多时能简化电路设计,减少组合逻辑的复杂度。
1-Hot State Encoding Example
在1-hot编码中,每个状态使用一组位来表示,且在任何时刻只有一个位为1,其余位为0。例如:
- 状态
S0用0001表示。 - 状态
S1用0010表示。 - 状态
S2用0100表示。 - 状态
S3用1000表示。
表格展示了基于1-hot编码的状态转移:
- 当前状态用一组1-hot编码表示。
- 根据传感器输入
T_A和T_B的值,FSM决定下一个状态的编码。
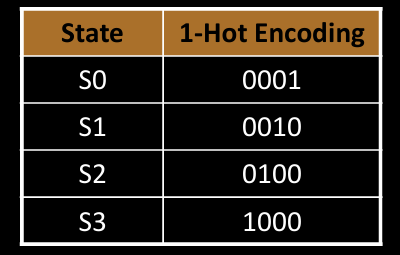
这种编码方式在硬件实现中经常被使用,尤其在需要快速状态转移和简化逻辑的场景中。
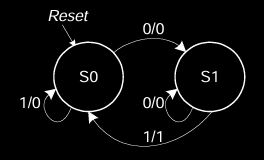
Mealy FSM Example
Moore vs. Mealy FSMs
在这个例子中,Alyssa P. Hacker设计了一个蜗牛控制系统。蜗牛爬过一张纸带,纸带上有1和0组成的序列。每当蜗牛爬过的最后两位是01时,蜗牛就会微笑。目标是为这个系统设计摩尔(Moore)和米利(Mealy)有限状态机(FSM)。
- Moore FSM:输出只依赖当前状态。换句话说,只有当状态满足特定条件时,蜗牛才会微笑。
- Mealy FSM:输出依赖于当前状态和输入。这样,蜗牛的微笑可能会更迅速地响应输入变化。
Moore FSM State Transition Table
摩尔状态机的状态转移表列出了当前状态与输入条件下,FSM如何决定下一个状态:
- 当前状态:
S1和S0代表当前的状态编码。每个状态用二进制数编码,例如S0为00,S1为01,S2为10。 - 输入(A):输入值决定状态机的转移。例如,当输入
A=0时,FSM从S0转移到S1。 - 下一状态:在每种输入条件下,FSM的下一状态由状态转移逻辑决定。
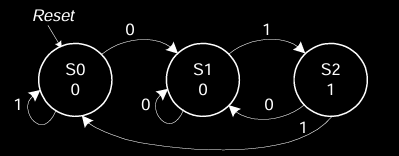
例如:
- 当状态机处于
S0(00)状态,且输入为A=0时,FSM保持在S0。 - 当状态机处于
S0,且输入为A=0时,FSM转移到S1(01)。
Moore FSM Encoding
摩尔状态机的每个状态都有对应的二进制编码:
- S0:
00 - S1:
01 - S2:
10
这种编码方式允许状态机根据输入进行状态转移,同时输出仅依赖于当前状态的值。
Moore FSM Output Table
在摩尔状态机中,输出仅依赖于当前状态,与输入无关。以下是该FSM的输出表:
- 当前状态:
S1和S0代表状态机的状态。例如:S0 = 00,表示状态S0。S1 = 01,表示状态S1。S2 = 10,表示状态S2。
- 输出(Y):摩尔FSM的输出由状态决定。在这个例子中,只有在
S2状态下,输出Y = 1。
例如,当状态为S0或S1时,输出为Y = 0;当状态为S2时,输出为Y = 1。
Mealy State Transition & Output Table
在米利状态机中,输出不仅依赖于当前状态,还取决于输入。以下是该FSM的状态转移和输出表:
- 当前状态:
S0和S1是状态机的状态。 - 输入(A):当前输入决定了下一状态以及输出。
- 下一个状态(S’0):根据当前状态和输入,状态机会转移到下一个状态。
- 输出(Y):根据当前状态和输入,产生的输出。例如:
- 如果当前状态为
S0,且A = 1,则输出Y = 1。
- 如果当前状态为
因此,米利状态机可以在状态改变之前根据输入产生输出,这使得它的响应更加灵敏。
Moore FSM Schematic
摩尔状态机的电路图基于以下逻辑方程:
- 下一状态方程:
S1' = S0 * A:下一个状态S1'由当前状态S0和输入A决定。S0' = S0̅:下一个状态S0'是S0的反相。
- 输出方程:
Y = S1:输出Y完全由S1的状态决定。
Mealy FSM Schematic
米利状态机的电路图基于以下逻辑方程:
- 下一状态方程:
S0' = A̅:下一个状态S0'取决于输入A的反相。
- 输出方程:
Y = S0 * A:输出Y同时依赖于当前状态S0和输入A。
这种设计使得米利状态机能在输入变化时立即产生输出,而不必等到状态改变。
Moore and Mealy Timing Diagram
时序图展示了摩尔(Moore)和米利(Mealy)有限状态机(FSM)在多个时钟周期中的状态和输出变化:
-
摩尔FSM:输出
Y仅依赖于当前状态,因此当输入序列01被检测到时,状态机会转移到相应状态,并在下一个时钟周期输出Y=1。因此,摩尔FSM的输出有一个时钟周期的延迟。 -
米利FSM:输出
Y依赖于当前状态和输入,因此一旦检测到输入序列01,状态机会立即输出Y=1。这使得米利FSM的响应速度更快,可以在状态转移之前生成输出。

在图中,米利FSM的输出比摩尔FSM更早更新,反映了它的输出对输入的敏感性。
Factored FSMs
Factoring FSMs
分解FSM(Factored FSMs)是一种将复杂的FSM划分为多个较小的、互相协作的FSM的方法。这种方法能够简化设计、提高模块化,并让每个子FSM独立处理不同的功能。
Parade Mode Example
在该例子中,将交通灯控制器FSM修改为包含一个游行模式(Parade Mode)。通过分解,FSM将被分成两个独立的FSM:
- Mode FSM:负责处理模式切换。当输入
P=1时,系统进入游行模式,Bravado Blvd的灯光保持绿灯。当R=1时,系统离开游行模式。 - Lights FSM:控制交通灯的状态,决定每个方向的交通灯状态(
L_A和L_B)。
Parade FSMs
-
未分解FSM(Unfactored FSM):这是传统的设计方式,所有功能都由一个单一的FSM控制。输入
P、R、T_A和T_B直接影响输出交通灯信号L_A和L_B。 -
分解FSM(Factored FSM):通过分解,控制器被分成Mode FSM和Lights FSM两个子FSM。Mode FSM决定系统是否处于游行模式,并通过信号
M影响Lights FSM。Lights FSM负责实际的交通灯控制,而Mode FSM则根据游行模式和状态切换来影响其决策。
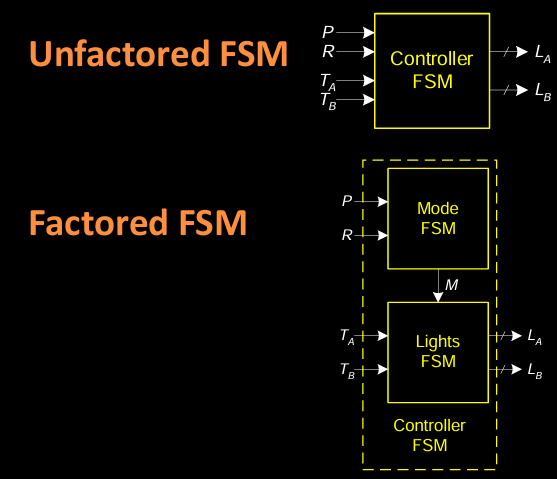
这种分解方式使系统更加模块化、易于管理,同时每个子FSM负责处理特定功能,降低了复杂度。
Unfactored FSM
未分解的FSM设计图显示了一个复杂的交通灯控制系统,所有的状态和状态转换都在一个单一的FSM中进行管理。这种设计虽然能够处理系统的所有功能,但随着系统复杂度的增加,状态和转换的数量大幅增长,变得难以管理。FSM的各个状态对应不同的交通灯配置:
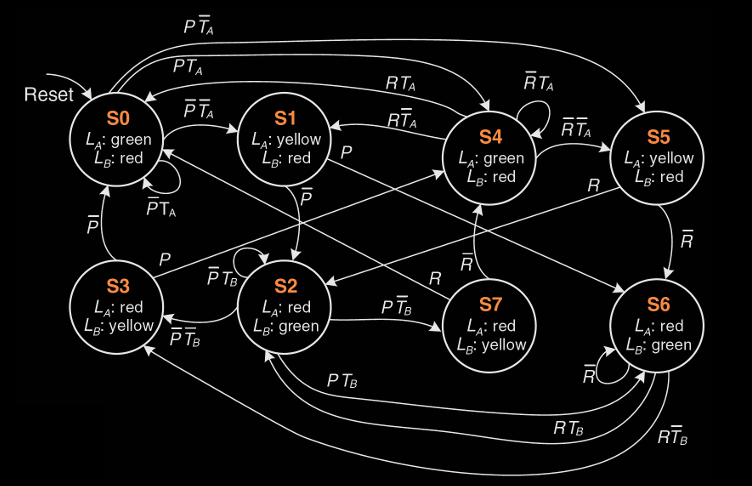
- 状态S0:方向A绿灯,方向B红灯。
- 状态S1:方向A黄灯,方向B红灯。
- 其他状态也有类似的灯光配置。
输入信号P、R、T_A和T_B决定了不同状态之间的转移。
Factored FSM
分解后的FSM将复杂的FSM分成了两个较小的FSM:Mode FSM 和 Lights FSM。
-
Mode FSM 负责系统是否进入游行模式。当
P=1时,进入游行模式,R=1时退出游行模式。游行模式通过信号M传递给Lights FSM。 -
Lights FSM 控制交通灯的正常切换。它根据传感器输入
T_A和T_B以及Mode FSM的输出M来控制灯的状态变化。在游行模式下,Bravado Blvd的灯保持绿灯。
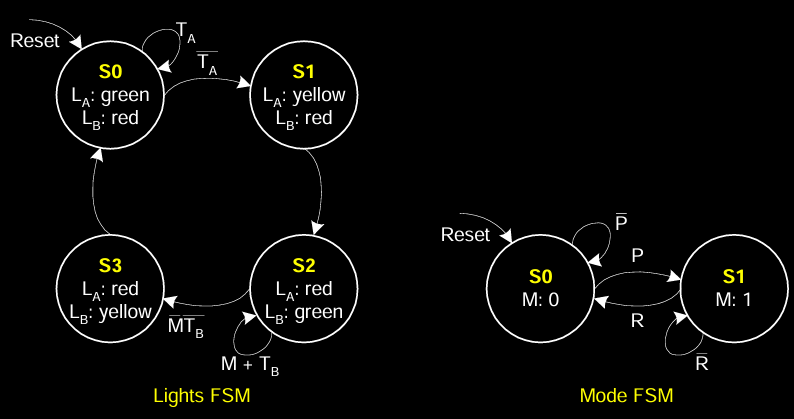
这种分解方式将复杂的系统模块化,使得每个子FSM负责处理特定功能,极大简化了系统设计和管理。
Timing
时序在时序逻辑设计中至关重要,尤其是在触发器(如D触发器)中:
- D触发器在时钟的上升或下降沿采样输入信号
D,并在下一时钟周期更新输出。 - 采样时稳定性:在时钟边沿采样时,输入信号
D必须保持稳定,类似于拍摄照片时物体必须保持静止,以避免模糊。 - 稳定窗口:信号
D需要在时钟边沿的某个时间窗口内保持稳定,否则会导致不稳定的输出或错误。
这种时序要求确保系统在时钟的控制下有序运行,防止因为输入信号的变化导致错误的状态转移。
Input Timing Constraints
在时序逻辑电路中,输入信号必须满足特定的时间约束,才能确保数据正确地被锁存器采样并处理。这些约束包括:
-
建立时间(Setup Time, t_setup):数据
D必须在时钟边沿到来之前稳定的最小时间。例如,在时钟上升沿采样数据前,数据需要在t_setup时间内保持稳定,不能发生变化。 -
保持时间(Hold Time, t_hold):时钟边沿到来后,数据
D需要继续保持稳定的最小时间,确保触发器正确地采样数据。 -
孔径时间(Aperture Time, t_a):这是围绕时钟边沿的数据稳定时间段,等于建立时间和保持时间之和,
t_a = t_setup + t_hold。在孔径时间内,数据D必须保持稳定。
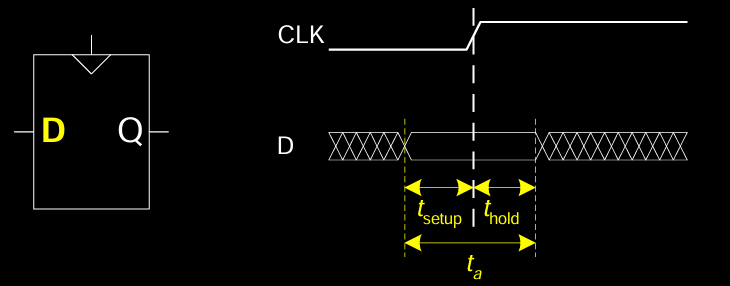
时序图展示了触发器如何在时钟边沿采样数据,并强调了数据需要在时钟采样前后的一定时间内保持不变。
Output Timing Constraints
除了输入时序,输出信号也存在相关的时间约束:
-
传播延迟(Propagation Delay, t_pcq):时钟边沿后,输出
Q需要一段时间才能稳定,这段时间称为传播延迟,是输出达到稳定的最大时间。 -
污染延迟(Contamination Delay, t_ccq):这是最小延迟时间,指在时钟边沿之后,输出可能开始不稳定的时间段。在此之前,输出可能发生变化。
这些输出时间约束确保电路设计的同步性,使得下一级电路在预期时间获得稳定的输出。
Dynamic Discipline
动态规范确保同步时序电路的输入在孔径时间内保持稳定,避免时序错误:
- 输入信号必须在时钟边沿之前至少有
t_setup时间的稳定期,并在时钟边沿之后至少有t_hold时间的稳定期。
如果输入不满足这些约束,可能会导致触发器采样到不正确的信号值,进而导致系统错误。
Timing Between Registers
寄存器之间的信号传输时间也存在最小和最大延迟要求,这取决于电路中元件的延迟。寄存器之间的时序设计必须考虑:
- 最小延迟:确保信号在下一个寄存器采样前有足够的时间稳定。
- 最大延迟:确保信号不会过晚到达而导致下一时钟周期内的数据无法正确采样。
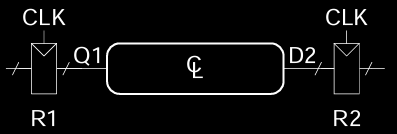
这个时序约束在复杂的同步电路中尤为重要,尤其是寄存器之间有多个逻辑元件时。
Setup Time Constraint
建立时间约束依赖于寄存器R1通过组合逻辑到达寄存器R2的最大延迟:
- 输入信号到达寄存器R2的时间必须在时钟边沿前至少保持稳定一段时间,称为建立时间(t_setup)。
- 如果信号没有在
t_setup时间前稳定,寄存器R2可能无法正确采样数据。
该约束也被称为时钟周期约束,因为它决定了寄存器之间的信号传播所需的最小时钟周期。
Hold Time Constraint
保持时间约束依赖于寄存器R1通过组合逻辑到寄存器R2的最小延迟:
- 输入信号在时钟边沿后,必须继续保持稳定一段时间,称为保持时间(t_hold)。
- 如果信号没有保持足够长的时间,寄存器R2可能会错误地采样信号,导致不可靠的行为。
保持时间约束要求信号在时钟边沿之后稳定一段时间,以确保数据被正确锁存。
Timing Analysis
在时序分析中,需要同时计算两种约束:
- 建立时间约束(即周期时间约束):决定时钟周期必须至少多长,才能确保信号在时钟边沿之前正确到达。
- 保持时间约束:确保信号在时钟边沿之后不会立即变化。
如果保持时间约束没有满足,无论时钟频率如何,电路都无法正常工作。这是时序设计中最为严格的要求之一。
Timing Analysis Example
时序分析例子展示了一个包含多个逻辑门和触发器的电路:
- 触发器的时间参数:包括时钟到Q延迟(t_ccq = 30 ps)、传播延迟(t_pcq = 50 ps)、建立时间(t_setup = 60 ps)、保持时间(t_hold = 70 ps)。
- 逻辑门延迟:每个逻辑门的传播延迟(t_pd = 35 ps)、污染延迟(t_cd = 25 ps)。
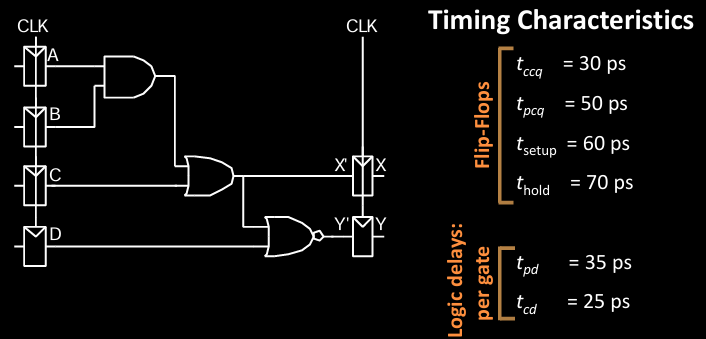
通过这些时序参数,可以计算出信号在该组合逻辑电路中的总传播延迟和时钟周期要求,确保设计能够正确工作。
在此时序分析例子中,我们要解决的核心问题是如何满足建立时间约束和保持时间约束,确保电路在时钟周期内能够正确工作:
-
逻辑延迟(Logic Delays):通过三个逻辑门的总延迟为
3 x 35 ps = 105 ps。此外,逻辑门还具有污染延迟t_cd = 25 ps。 -
触发器特性:包含以下延迟时间:
- t_ccq = 30 ps:时钟到Q的污染延迟。
- t_pcq = 50 ps:时钟到Q的传播延迟。
- t_setup = 60 ps:建立时间。
- t_hold = 70 ps:保持时间。
通过这些延迟信息,可以计算满足时序要求的最短和最长时钟周期,确保电路不会由于时序问题而失效。
如何解决?
- 建立时间约束:计算信号从寄存器输出(Q1)到达下一个寄存器输入(D2)的最大延迟,确保信号能在下一个时钟边沿前稳定。
- 保持时间约束:确保信号在时钟边沿后保持稳定足够长的时间,以避免误读数据。
Clock Skew
时钟偏斜(Clock Skew)是指时钟信号在不同寄存器间的到达时间差异。时钟偏斜会影响电路的时序,并可能导致系统失效,尤其是在大规模系统中,时钟偏斜会显著增加:
-
偏斜(Skew):是两个时钟边沿之间的差异。理想情况下,时钟信号应同时到达所有寄存器,但实际中,由于布线和电路延迟的差异,不同寄存器会在不同时间收到时钟信号。
-
最坏情况分析:为了确保动态规范不被违反,需要进行最坏情况下的时序分析,假设所有寄存器的时钟信号均存在最大偏斜,以确保系统在任何条件下都能可靠工作。
Setup Time Constraint with Skew
在有时钟偏斜的情况下,时序分析变得更复杂:
-
在最坏情况下,时钟信号
CLK2比CLK1提前到达。这种偏斜可能会缩短信号的建立时间,导致信号无法在下一个时钟边沿前稳定。 -
建立时间约束变为:
T_c - t_skew,即实际可用的建立时间是时钟周期减去偏斜时间。
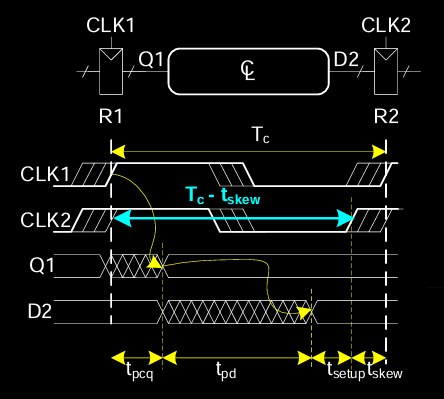
为了确保系统在时钟偏斜条件下仍然能正常工作,需要在时序设计中考虑这种偏斜,并根据偏斜对时钟周期和建立时间做出调整。
Hold Time Constraint with Skew
在有时钟偏斜的情况下,保持时间约束的复杂度增加:
- 在最坏情况下,时钟信号
CLK2比CLK1延迟到达。这意味着寄存器R2会比R1稍晚接收到时钟信号。

-
保持时间约束:信号必须在时钟边沿后稳定一段时间,具体来说,保持时间
t_hold必须足够长,才能弥补时钟偏斜带来的延迟。 -
如果时钟
CLK2的偏移量t_skew较大,信号可能会在下一个时钟边沿到来前发生变化,导致保持时间不满足要求,从而引发系统不稳定。
因此,时钟偏斜会对保持时间产生直接影响,设计中必须考虑到这种情况,确保在偏斜条件下仍能满足保持时间约束。
Synchronization
同步是时序逻辑电路中的关键问题,尤其当不同信号来自不同的时钟域时。输入信号往往是不同步的,尤其是在用户输入或其他外部信号进入系统时。这可能导致动态规范被违反。
Violating the Dynamic Discipline
异步输入(例如用户按下按钮)的不确定时间可能会导致动态规范被违反。这意味着输入信号无法按照预期的时间到达,可能导致系统无法正确采样输入。
-
异步输入:例如用户按下按钮,可能与时钟信号不同步。这样,输入信号在采样时可能恰好处于建立时间或保持时间之外,导致信号不稳定。
-
三种情况:右侧时序图展示了三种可能的情况:
- Case I:输入信号
D在建立时间和保持时间内保持稳定,系统正常工作。 - Case II:输入信号
D在时钟边沿时恰好发生变化。 - Case III:输入信号在采样窗口内不稳定,系统可能会进入不确定的状态。
- Case I:输入信号
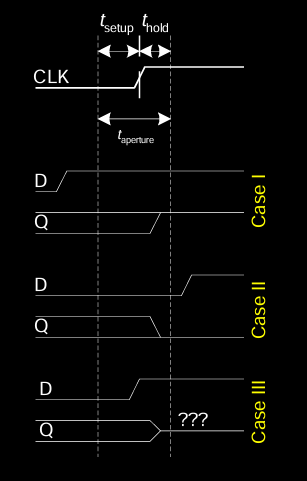
为了避免动态规范的违反,通常会使用同步器来将异步输入与时钟信号同步。
Metastability
亚稳态(Metastability)是指触发器在两个稳定状态之间进入一种不稳定的中间状态。
-
双稳态设备(Bistable Devices):例如触发器(Flip-Flop)有两个稳定状态,分别对应输出
1和0,但是在这两个稳定状态之间还有一个亚稳态,即不确定的状态。 -
如果输入信号在建立时间或保持时间内不稳定,触发器可能会进入这个亚稳态。亚稳态可能持续一段不确定的时间,直到系统最终返回到稳定状态。
亚稳态可能会引发不可预测的系统行为,特别是在高频系统或异步信号输入的情况下。因此,设计中必须通过正确的同步机制来减少亚稳态的发生概率。
Flip-Flop Internals
触发器(Flip-Flop)的内部结构依赖于反馈机制来维持稳定输出:
-
反馈机制:如果输出
Q处于1和0之间的亚稳态,交叉耦合门(如NAND门或NOR门)会驱动输出进入稳定状态,即输出要么变为逻辑1,要么变为逻辑0。 -
亚稳态信号:如果触发器的输入在建立时间或保持时间之外发生变化,输出
Q可能进入亚稳态,而不是立即解析为1或0。 -
亚稳态持续时间的概率:触发器在采样输入信号后,输出
Q可能进入亚稳态。其持续时间t_res服从指数分布:[ P(t_{res} > t) = \left( \frac{T_0}{T_c} \right) e^{-t/\tau} ]
其中:
- ( T_0 ) 和 ( \tau ) 是电路的特性常数,描述了触发器从亚稳态恢复的速度。
- ( t_res ) 是输出解析为1或0的时间。
Metastability
亚稳态可以用直观的方式理解为,输入信号在建立时间或保持时间内变化,导致触发器无法确定输出是1还是0。
-
亚稳态概率公式:输入在建立时间和保持时间内不稳定,导致触发器进入亚稳态的概率为:
[ P(t_{res} > t) = \left( \frac{T_0}{T_c} \right) e^{-t/\tau} ]
该公式表明,随着等待时间
t的增加,触发器从亚稳态恢复到稳定状态的概率呈指数下降。 -
重要性:如果等待足够长的时间,触发器的输出最终会以很高的概率解析为1或0。
Synchronizers
在复杂的数字系统中,异步输入不可避免,例如用户输入或不同时钟域之间的交互。异步信号可能导致动态规范被违反,触发器采样到亚稳态信号。
-
同步器的目标:同步器的目的是通过延长信号的传播时间来降低亚稳态的发生概率,确保系统可靠工作。
-
概率控制:虽然同步器不能完全消除亚稳态的风险,但它可以显著降低触发器采样到亚稳态信号的概率,使系统的可靠性提高。
同步器的设计通过增加触发器级数或延长信号传播时间来确保异步信号能够被正确采样,并减少亚稳态对系统的影响。
Synchronizer Internals
同步器是为了处理异步信号和同步时钟域的相互转换而设计的电路,常用的同步器由两个级联的触发器(Flip-Flops)组成,确保输入信号在进入系统之前得到可靠采样。
-
同步器结构:同步器由两个级联的D触发器组成,第一个触发器(F1)采样异步输入
D,第二个触发器(F2)进一步处理来自F1的信号D2,并输出稳定信号Q。 -
亚稳态的处理:假设输入
D在F1采样时发生了变化,F1的输出信号D2可能会进入亚稳态。在这种情况下,D2必须在一定的时间内解析为稳定的逻辑值(1或0)。 -
时间窗口:信号
D2有足够的时间来解析为稳定状态,即时钟周期(Tc)减去建立时间(t_setup)的时间。这样可以保证同步器输出的信号Q最终是可靠的。
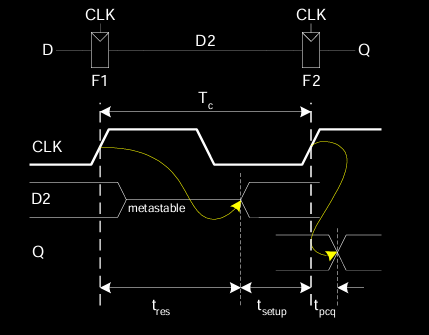
Synchronizer Probability of Failure
尽管同步器可以显著降低亚稳态对系统的影响,但它不能完全消除亚稳态发生的可能性。每次采样信号时,仍然存在一定的失败概率,即同步器无法在指定时间内解析信号的概率。
-
失败概率公式:
[ P(\text{failure}) = \left( \frac{T_0}{T_c} \right) e^{-(T_c - t_{\text{setup}})/\tau} ]
其中:
- ( T_0 ) 是与电路特性相关的时间常数。
- ( T_c ) 是时钟周期。
- ( t_{\text{setup}} ) 是触发器的建立时间。
- ( \tau ) 是电路移出亚稳态的时间常数。
该公式说明了信号进入亚稳态并且未在规定时间内解析为稳定状态的概率。随着时钟周期的增大或建立时间的缩短,亚稳态发生的概率会减小。
-
时间图:图中展示了信号
D2进入亚稳态的情况,以及从亚稳态恢复的过程。D2有一段时间t_res解析为稳定状态,并在下一个时钟边沿由F2触发器采样后,最终输出信号Q。
同步器的设计目标是使这种失败的概率足够小,从而使系统能够在实际应用中可靠运行。然而,即使同步器经过精心设计,失败概率永远不可能降为零。
Synchronizer Mean Time Between Failure (MTBF)
同步器的设计目标是确保异步输入信号被可靠采样,然而,完全消除失败的可能性是不现实的。为了衡量同步器的可靠性,我们使用平均故障间隔时间(Mean Time Between Failure, MTBF),它表示同步器在发生一次故障之前的平均工作时间。
-
失败概率/秒:如果异步输入每秒变化一次,失败的概率是
P(failure)。如果输入信号每秒发生N次变化,则每秒的失败概率为:[ P(failure)/\text{second} = \left( \frac{NT_0}{T_c} \right) e^{-(T_c - t_{\text{setup}})/\tau} ]
-
MTBF计算:同步器的平均故障间隔时间是失败概率的倒数,即:
[ MTBF = \frac{1}{P(failure)/\text{second}} = \frac{T_c}{NT_0} e^{(T_c - t_{\text{setup}})/\tau} ]
这意味着随着时钟周期增加或信号变化频率降低,MTBF会增加,系统变得更加可靠。
Example Synchronizer
让我们通过一个例子来计算同步器的失败概率和MTBF:
- 假设:
- ( T_c = 2 \, \text{ns} ) (时钟周期为500 MHz)
- ( T_0 = 150 \, \text{ps} ) (电路常数)
- ( \tau = 200 \, \text{ps} ) (电路从亚稳态恢复的时间常数)
- ( t_{\text{setup}} = 100 \, \text{ps} ) (建立时间)
- ( N = 10 ) (输入信号每秒变化10次)

在这些参数下,我们可以计算出失败概率和MTBF,帮助评估同步器的可靠性。
Parallelism
并行性是时序逻辑设计中的一个重要概念,旨在通过同时执行多个任务来提高系统性能。并行性可以分为两种类型:
-
空间并行性(Spatial Parallelism):指多个任务在同一时刻在不同的硬件资源上同时进行。它通常通过增加硬件资源来实现,例如多核处理器或多线程架构。
-
时间并行性(Temporal Parallelism):指一个任务分成多个阶段,多个阶段在不同的时间段内并行执行。流水线是时间并行性的一种常见实现方式,在每个时钟周期内,各阶段同时处理不同的数据。
Parallelism
并行性通过允许多个任务同时进行来提高系统的性能,它能够显著增加吞吐量(Throughput),即单位时间内完成的工作量。然而,延迟(Latency)是指从开始到结束完成一个任务所需的时间,它并不会直接因为并行性而减少。
- Token:并行处理的基本单位,可以理解为一组输入数据经过处理后得到的一组输出数据。
- 延迟:指一个token从输入到输出的整个处理时间。延迟主要反映的是单个任务的完成时间。
- 吞吐量:指单位时间内系统能够处理的token数量。并行处理通常通过提高吞吐量来加快总体处理速度。
并行性的主要优点之一就是能够提高吞吐量,这意味着即使延迟不变,系统能够在相同时间内处理更多的数据。
Parallelism Example
在这个例子中,Ben正在烤饼干来庆祝交通灯控制器的安装:
- 准备时间:滚动饼干团需要5分钟。
- 烘焙时间:烤饼干需要15分钟。
Without Parallelism
假设Ben一次只能处理一盘饼干,那么:
- 延迟:一盘饼干从准备到烘焙完成需要 5 + 15 = 20分钟。
- 吞吐量:每20分钟可以完成1盘饼干的制作。
With Parallelism
如果Ben使用并行处理,可以大幅提高效率。
-
空间并行性(Spatial Parallelism):Ben请求Alyssa P. Hacker的帮助,使用她的烤箱同时烘焙两盘饼干。这样一次可以同时烘焙两盘,吞吐量翻倍。
-
时间并行性(Temporal Parallelism):Ben使用两盘饼干托盘,并将准备和烘焙分为两个阶段。在第一批饼干烘焙的同时,他准备第二批饼干。这样,当第一批饼干烘焙完成时,第二批也已经准备好放入烤箱。
通过这两种并行方式,Ben的饼干制作效率得到了显著提高。空间并行性使他同时处理多盘饼干,而时间并行性则使他能更高效地利用时间,从而进一步增加了整体的吞吐量。
Spatial Parallelism
在空间并行性中,Ben和Alyssa同时使用各自的烤箱来制作饼干。这种并行方式的关键在于同时处理多个任务,而不是依次处理。
- 延迟(Latency):第一个托盘的完成时间。根据图示,Ben和Alyssa几乎同时开始滚动和烘焙他们的托盘。第一个托盘的延迟是 20分钟。
- 吞吐量(Throughput):通过并行处理,Ben和Alyssa每 20分钟 可以烘焙 2个托盘,因此吞吐量显著提高。
Temporal Parallelism
时间并行性通过分解任务阶段并流水化处理各个任务来提高效率。例如,Ben使用两个托盘,第一个托盘正在烘焙时,他开始准备第二个托盘,第二个托盘进烤箱时,Ben又准备好了第三个托盘。
- 延迟(Latency):第一个托盘从开始到完成的时间依旧是 20分钟。
- 吞吐量(Throughput):由于Ben能够在烘焙的同时准备新的托盘,因此 每15分钟 可以完成一个托盘,显著提高了吞吐量。
通过这两种并行方式,无论是空间并行性还是时间并行性,都能够极大地提升系统的吞吐量,虽然延迟不变,但能够在单位时间内完成更多任务,从而加快整体工作流程。
Digital Design and Computer Architecture Lecture Notes © 2021 Sarah Harris and David Harris
These notes may be used and modified for educational and/or non-commercial purposes so long as the source is attributed.